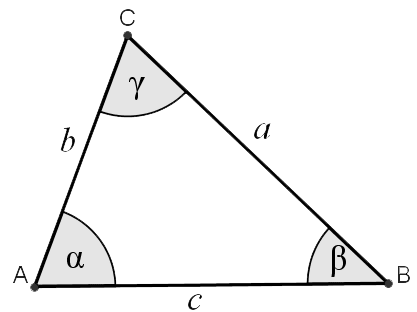
Výpočet trojúhelníku - výsledek

Zadané strany a, c a výška v_c.

Trojúhelník má dvě řešení: a=5; b=16.27988205961; c=12 a a=5; b=8.54440037453; c=12.

#1 Tupouhlý různostranný trojúhelník.

Strany: a = 5 b = 16,27988205961 c = 12

Obsah trojúhelníku: S = 18
Obvod trojúhelníku: o = 33,27988205961
Semiperimeter (poloobvod): s = 16,6399410298

Úhel ∠ A = α = 10,62196552762° = 10°37'11″ = 0,185534795 rad
Úhel ∠ B = β = 143,13301023542° = 143°7'48″ = 2,49880915448 rad
Úhel ∠ C = γ = 26,25502423697° = 26°15'1″ = 0,45881531588 rad

Výška trojúhelníku: v_a = 7,2
Výška trojúhelníku: v_b = 2,21114624206
Výška trojúhelníku: v_c = 3

Těžnice: t_a = 14,08801278403
Těžnice: t_b = 4,27220018727
Těžnice: t_c = 10,44403065089

Poloměr vepsané kružnice: r = 1,08217691059
Poloměr opsané kružnice: R = 13,56656838301

Souřadnice vrcholů: A[12; 0] B[0; 0] C[-4; 3]
Těžiště: T[2,66766666667; 1]
Souřadnice středu kružnice opsané: U[6; 12,16766666667]
Souřadnice středu vepsané kružnice: I[0,3610589702; 1,08217691059]

Vnější úhly trojúhelníku:
∠ A' = α' = 169,38803447238° = 169°22'49″ = 0,185534795 rad
∠ B' = β' = 36,87698976458° = 36°52'12″ = 2,49880915448 rad
∠ C' = γ' = 153,75497576303° = 153°44'59″ = 0,45881531588 rad

Jak jsme vypočítali tento trojúhelník?

Výpočet trojúhelníku probíhá ve dvou fázích. První fáze je taková, že ze vstupních parametrů se snažíme vypočítat všechny tři strany trojúhelníku. První fáze probíhá různě pro různé zadané trojúhelníky. Druhá fáze je vlastně výpočet ostatních charakteristik trojúhelníku (z již vypočtených stran, proto SSS), jako jsou úhly, plocha, obvod, výšky, těžnice, poloměry kružnic atd. Některé vstupní vstupní údaje vedou i ke dvěm až třem správným řešením trojúhelníku (např. pokud je zadaný obsah trojúhelníku a dvě strany - výsledkem je typicky ostroúhlý a tupoúhlý trojúhelník).

1. Zadané vstupní údaje: strany a, c a výška v_c.

a = 5 c = 12 v_{c} = 3

2. Ze strany c a výšky v_c vypočítáme obsah S:

S = \frac{c v _{c}}{2} S = \frac{1 2 \cdot 3}{2} = 18

Nyní, když víme délky všech tří stran trojúhelníku, trojúhelník je jednoznačně určen. Dále proto výpočet je stejný a dopočítají se další jeho vlastnosti - výpočet trojúhelníku ze známých tří stran SSS.

a = 5 b = 16, 28 c = 12

3. Obvod trojúhelníku je součtem délek jeho tří stran

o = a + b + c = 5 + 16, 28 + 12 = 33, 28

4. Poloviční obvod trojúhelníku

Poloviční obvod trojúhelníku (semiperimeter) je polovina z jeho obvodu. Poloviční obvod trojúhelníku se ve vzorcích pro trojúhelníky často vyskytuje tak, že mu byl přidělen samostatný název (semiperimeter - poloobvod - s). Trojúhelníková nerovnost říká, že nejdelší délka strany trojúhelníku musí být menší než semiperimeter.

s = \frac{o}{2} = \frac{3 3 , 2 8}{2} = 16, 64

5. Obsah trojúhelníku pomocí Heronova vzorce

Heronův vzorec dává obsah trojúhelníku, kdy jsou známé délky všech tří stran. Není třeba nejprve vypočítat úhly nebo jiné vzdálenosti v trojúhelníku. Heronův vzorec funguje stejně dobře ve všech případech a druzích trojúhelníků.

S = s (s - a) (s - b) (s - c) S = 16, 64 (16, 64 - 5) (16, 64 - 16, 28) (16, 64 - 12) S = 324 = 18

6. Výpočet výšek trojúhelníku z jeho obsahu.

Existuje mnoho způsobů, jak zjistit výšku trojúhelníku. Nejjednodušší způsob je ze vzorce, když známe obsah a délku základny. Plocha trojúhelníku je polovinou součinu délky základny a výšky. Každá strana trojúhelníku může být základnou; existují tedy tři základny a tři výšky. Výška trojúhelníku je kolmá úsečka od vrcholu po přímku obsahující základnu.

S = \frac{a v _{a}}{2} v_{a} = \frac{2 S}{a} = \frac{2 \cdot 1 8}{5} = 7, 2 v_{b} = \frac{2 S}{b} = \frac{2 \cdot 1 8}{1 6 , 2 8} = 2, 21 v_{c} = \frac{2 S}{c} = \frac{2 \cdot 1 8}{1 2} = 3

7. Výpočet vnitřních úhlů trojúhelníku pomocí kosinové věty

Kosinová věta je užitečná při hledání úhlů trojúhelníku, když známe všechny tři strany. Kosinová věta spojuje všechny tři strany trojúhelníku s úhlem trojúhelníku. Kosinová věta je extrapolací Pythagorovy věty pro jakýkoliv trojúhelník. Pythagorova věta funguje pouze v pravoúhlém trojúhelníku. Pythagorova věta je zvláštním případem kosinové věty a dá se z něj odvodit, protože kosinus 90 ° je 0. Nejlepší je nejprve najít úhel oproti nejdelší straně. V případě kosinové věty neexistuje problém s tupými úhly jako v případě sinusové věty, protože funkce kosinus je záporná pro tupé úhly, nulová pro pravé a kladná pro ostré úhly. K určení úhlu z hodnoty kosinus používáme inverzní kosinus nazývaný arkuskosinus.

a^{2} = b^{2} + c^{2} - 2 b c cos α α = arccos (\frac{b ^{2} + c ^{2} - a ^{2}}{2 b c}) = arccos (\frac{1 6 , 2 8 ^{2} + 1 2 ^{2} - 5 ^{2}}{2 \cdot 1 6 , 2 8 \cdot 1 2}) = 10 ° 3 7^{'} 11 " b^{2} = a^{2} + c^{2} - 2 a c cos β β = arccos (\frac{a ^{2} + c ^{2} - b ^{2}}{2 a c}) = arccos (\frac{5 ^{2} + 1 2 ^{2} - 1 6 , 2 8 ^{2}}{2 \cdot 5 \cdot 1 2}) = 143 ° 7^{'} 48 " γ = 180 ° - α - β = 180 ° - 10 ° 3 7^{'} 11 " - 143 ° 7^{'} 48 " = 26 ° 1 5^{'} 1 "

8. Poloměr vepsané kružnice

Vepsaná kružnice v trojúhelníku je kružnice (kruh), který se dotýká každé jeho strany. Všechny trojúhelníky mají vepsanou kružnici a její střed vždy leží uvnitř trojúhelníku. Střed vepsané kružnice je průsečík tří os vnitřních úhlů (průsečík bisektorov). Součin poloměru vepsané kružnice a semiperimetru (poloviny obvodu) trojúhelníku je jeho plocha.

S = r s r = \frac{S}{s} = \frac{1 8}{1 6 , 6 4} = 1, 08

9. Poloměr opsané kružnice

Opsaná kružnice trojúhelníku je kružnice, která prochází všemi vrcholy trojúhelníku. Střed opsané kružnice je bod, ve kterém se protínají osy stran trojúhelníku.

R = \frac{a b c}{4 r s} = \frac{5 \cdot 1 6 , 2 8 \cdot 1 2}{4 \cdot 1 , 0 8 2 \cdot 1 6 , 6 3 9} = 13, 57

10. Výpočet těžnic

Těžnice (medián) trojúhelníku je úsečka spojující vrchol se středem protější strany. Každý trojúhelník má tři těžnice a všechny se vzájemně protínají v těžišti trojúhelníku. Těžiště rozděluje těžnice na části v poměru 2: 1, přičemž těžiště je dvakrát blíže ke středu strany jako protilehlý vrchol. Apolloniusovu větu používáme pro výpočet délky těžnic z délek jeho stran.

t_{a} = \frac{2 b ^{2} + 2 c ^{2} - a ^{2}}{2} = \frac{2 \cdot 1 6 , 2 8 ^{2} + 2 \cdot 1 2 ^{2} - 5 ^{2}}{2} = 14, 08 t_{b} = \frac{2 c ^{2} + 2 a ^{2} - b ^{2}}{2} = \frac{2 \cdot 1 2 ^{2} + 2 \cdot 5 ^{2} - 1 6 , 2 8 ^{2}}{2} = 4, 272 t_{c} = \frac{2 a ^{2} + 2 b ^{2} - c ^{2}}{2} = \frac{2 \cdot 5 ^{2} + 2 \cdot 1 6 , 2 8 ^{2} - 1 2 ^{2}}{2} = 10, 44

#2 Tupouhlý různostranný trojúhelník.

Strany: a = 5 b = 8,54440037453 c = 12

Obsah trojúhelníku: S = 18
Obvod trojúhelníku: o = 25,54440037453
Semiperimeter (poloobvod): s = 12,77220018727

Úhel ∠ A = α = 20,55660452196° = 20°33'22″ = 0,35987706703 rad
Úhel ∠ B = β = 36,87698976458° = 36°52'12″ = 0,64435011088 rad
Úhel ∠ C = γ = 122,57440571346° = 122°34'27″ = 2,13993208745 rad

Výška trojúhelníku: v_a = 7,2
Výška trojúhelníku: v_b = 4,21334812991
Výška trojúhelníku: v_c = 3

Těžnice: t_a = 10,11218742081
Těžnice: t_b = 8,1399410298
Těžnice: t_c = 3,60655512755

Poloměr vepsané kružnice: r = 1,40993327091
Poloměr opsané kružnice: R = 7,12200031211

Souřadnice vrcholů: A[12; 0] B[0; 0] C[4; 3]
Těžiště: T[5,33333333333; 1]
Souřadnice středu kružnice opsané: U[6; -3,83333333333]
Souřadnice středu vepsané kružnice: I[4,22879981273; 1,40993327091]

Vnější úhly trojúhelníku:
∠ A' = α' = 159,44439547804° = 159°26'38″ = 0,35987706703 rad
∠ B' = β' = 143,13301023542° = 143°7'48″ = 0,64435011088 rad
∠ C' = γ' = 57,42659428654° = 57°25'33″ = 2,13993208745 rad

Vypočítat další trojúhelník

Jak jsme vypočítali tento trojúhelník?

1. Zadané vstupní údaje: strany a, c a výška v_c.

a = 5 c = 12 v_{c} = 3

2. Ze strany c a výšky v_c vypočítáme obsah S:

S = \frac{c v _{c}}{2} S = \frac{1 2 \cdot 3}{2} = 18

a = 5 b = 8, 54 c = 12

3. Obvod trojúhelníku je součtem délek jeho tří stran

o = a + b + c = 5 + 8, 54 + 12 = 25, 54

4. Poloviční obvod trojúhelníku

s = \frac{o}{2} = \frac{2 5 , 5 4}{2} = 12, 77

5. Obsah trojúhelníku pomocí Heronova vzorce

S = s (s - a) (s - b) (s - c) S = 12, 77 (12, 77 - 5) (12, 77 - 8, 54) (12, 77 - 12) S = 324 = 18

6. Výpočet výšek trojúhelníku z jeho obsahu.

S = \frac{a v _{a}}{2} v_{a} = \frac{2 S}{a} = \frac{2 \cdot 1 8}{5} = 7, 2 v_{b} = \frac{2 S}{b} = \frac{2 \cdot 1 8}{8 , 5 4} = 4, 21 v_{c} = \frac{2 S}{c} = \frac{2 \cdot 1 8}{1 2} = 3

7. Výpočet vnitřních úhlů trojúhelníku pomocí kosinové věty

a^{2} = b^{2} + c^{2} - 2 b c cos α α = arccos (\frac{b ^{2} + c ^{2} - a ^{2}}{2 b c}) = arccos (\frac{8 , 5 4 ^{2} + 1 2 ^{2} - 5 ^{2}}{2 \cdot 8 , 5 4 \cdot 1 2}) = 20 ° 3 3^{'} 22 " b^{2} = a^{2} + c^{2} - 2 a c cos β β = arccos (\frac{a ^{2} + c ^{2} - b ^{2}}{2 a c}) = arccos (\frac{5 ^{2} + 1 2 ^{2} - 8 , 5 4 ^{2}}{2 \cdot 5 \cdot 1 2}) = 36 ° 5 2^{'} 12 " γ = 180 ° - α - β = 180 ° - 20 ° 3 3^{'} 22 " - 36 ° 5 2^{'} 12 " = 122 ° 3 4^{'} 27 "

8. Poloměr vepsané kružnice

S = r s r = \frac{S}{s} = \frac{1 8}{1 2 , 7 7} = 1, 41

9. Poloměr opsané kružnice

Opsaná kružnice trojúhelníku je kružnice, která prochází všemi vrcholy trojúhelníku. Střed opsané kružnice je bod, ve kterém se protínají osy stran trojúhelníku.

R = \frac{a b c}{4 r s} = \frac{5 \cdot 8 , 5 4 \cdot 1 2}{4 \cdot 1 , 4 0 9 \cdot 1 2 , 7 7 2} = 7, 12

10. Výpočet těžnic

t_{a} = \frac{2 b ^{2} + 2 c ^{2} - a ^{2}}{2} = \frac{2 \cdot 8 , 5 4 ^{2} + 2 \cdot 1 2 ^{2} - 5 ^{2}}{2} = 10, 112 t_{b} = \frac{2 c ^{2} + 2 a ^{2} - b ^{2}}{2} = \frac{2 \cdot 1 2 ^{2} + 2 \cdot 5 ^{2} - 8 , 5 4 ^{2}}{2} = 8, 139 t_{c} = \frac{2 a ^{2} + 2 b ^{2} - c ^{2}}{2} = \frac{2 \cdot 5 ^{2} + 2 \cdot 8 , 5 4 ^{2} - 1 2 ^{2}}{2} = 3, 606

Vypočítat další trojúhelník

Výpočet trojúhelníku - výsledek

#1 Tupouhlý různostranný trojúhelník.

Jak jsme vypočítali tento trojúhelník?

1. Zadané vstupní údaje: strany a, c a výška vc.

2. Ze strany c a výšky vc vypočítáme obsah S:

3. Obvod trojúhelníku je součtem délek jeho tří stran

4. Poloviční obvod trojúhelníku

5. Obsah trojúhelníku pomocí Heronova vzorce

6. Výpočet výšek trojúhelníku z jeho obsahu.

7. Výpočet vnitřních úhlů trojúhelníku pomocí kosinové věty

8. Poloměr vepsané kružnice

9. Poloměr opsané kružnice

10. Výpočet těžnic

#2 Tupouhlý různostranný trojúhelník.

Jak jsme vypočítali tento trojúhelník?

1. Zadané vstupní údaje: strany a, c a výška vc.

2. Ze strany c a výšky vc vypočítáme obsah S:

3. Obvod trojúhelníku je součtem délek jeho tří stran

4. Poloviční obvod trojúhelníku

5. Obsah trojúhelníku pomocí Heronova vzorce

6. Výpočet výšek trojúhelníku z jeho obsahu.

7. Výpočet vnitřních úhlů trojúhelníku pomocí kosinové věty

8. Poloměr vepsané kružnice

9. Poloměr opsané kružnice

10. Výpočet těžnic

1. Zadané vstupní údaje: strany a, c a výška v_c.

2. Ze strany c a výšky v_c vypočítáme obsah S:

1. Zadané vstupní údaje: strany a, c a výška v_c.

2. Ze strany c a výšky v_c vypočítáme obsah S: