Obvodový úhel
Vrcholy trojúhelníku ΔABC vepsaného do kružnice ji dělí na oblouky v poměru 2:3:4. Určete velikosti vnitřních úhlů ΔABC.
Správná odpověď:
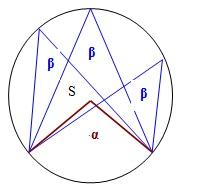
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- geometrie
- Thaletova věta
- středový a obvodový úhel
- planimetrie
- kruh, kružnice
- trojúhelník
- základní funkce
- úměra, poměr
- čísla
- zlomky
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Minutová 9
 Minutová ručička opíše za půl hodiny úhel 180 stupňů. Za kolik minut opíše minutová ručička úhel o velikosti 192 stupňů?
Minutová ručička opíše za půl hodiny úhel 180 stupňů. Za kolik minut opíše minutová ručička úhel o velikosti 192 stupňů?
- Mnohoúhelníku 81152
 V jistém mnohoúhelníku platí, že poměr součtu velikosti jeho vnitřních úhlů a součtu velikosti k nim doplňkových úhlů je 2:5. Kolik vrcholů má tento mnohoúhelník?
V jistém mnohoúhelníku platí, že poměr součtu velikosti jeho vnitřních úhlů a součtu velikosti k nim doplňkových úhlů je 2:5. Kolik vrcholů má tento mnohoúhelník? - V pravoúhlém 9
 V pravoúhlém trojúhelníku ABC (pravý úhel při vrcholu C ) je poměr úhlů α : β = 5 : 3. Vypočti velikosti těchto úhlů a převeď je na stupně a minuty (např. 45°20')
V pravoúhlém trojúhelníku ABC (pravý úhel při vrcholu C ) je poměr úhlů α : β = 5 : 3. Vypočti velikosti těchto úhlů a převeď je na stupně a minuty (např. 45°20') - Rovnoramenném 71154
 Vypočítejte všechny vnitřní úhly v rovnoramenném trojúhelníku ABC pokud víme, že BC je základna a navíc víme: |∢BAC|=α; |∢BCA|=4α
Vypočítejte všechny vnitřní úhly v rovnoramenném trojúhelníku ABC pokud víme, že BC je základna a navíc víme: |∢BAC|=α; |∢BCA|=4α - V trojúhelníku 6
 V trojúhelníku ABC jsou velikosti úhlů α, β γ v poměru 0,4 : 1 : 0,9. Vypočítejte jejich velikosti.
V trojúhelníku ABC jsou velikosti úhlů α, β γ v poměru 0,4 : 1 : 0,9. Vypočítejte jejich velikosti. - Vepsány čtyřúhelník
 Do kružnice je vepsán čtyřúhelník tak, že jeho vrcholy dělí kružnici 1:2:3:4. Vypočítejte velikosti jeho vnitřních úhlů.
Do kružnice je vepsán čtyřúhelník tak, že jeho vrcholy dělí kružnici 1:2:3:4. Vypočítejte velikosti jeho vnitřních úhlů.
- Velký kužel
 Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl?
Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl? - Velikosti 2
 Velikosti vnitřních úhlů trojúhelníku jsou v postupném poměru 6 : 4 : 5. Jak velké jsou tyto úhly?
Velikosti vnitřních úhlů trojúhelníku jsou v postupném poměru 6 : 4 : 5. Jak velké jsou tyto úhly? - Výpočty 2
 Výpočty z geometrie: Poměry stran čtyřúhelníku jsou 3 : 6:4,5 : 3,5. Vypočítejte jejich délky, jestliže obvod je 51 cm. Velikosti úhlů v čtyřúhelníku jsou = 29°30´, = 133°10´,= 165°20´. Jaká je velikost úhlu D?
Výpočty z geometrie: Poměry stran čtyřúhelníku jsou 3 : 6:4,5 : 3,5. Vypočítejte jejich délky, jestliže obvod je 51 cm. Velikosti úhlů v čtyřúhelníku jsou = 29°30´, = 133°10´,= 165°20´. Jaká je velikost úhlu D? - Výška
 Výška v a základny a, c v lichoběžníku ABCD jsou v poměru 1:6:3, jeho obsah S = 324 cm čtverečních. Úhel u vrcholu B = 35 stupňů. Určete obvod lichoběžníku
Výška v a základny a, c v lichoběžníku ABCD jsou v poměru 1:6:3, jeho obsah S = 324 cm čtverečních. Úhel u vrcholu B = 35 stupňů. Určete obvod lichoběžníku - Trojúhelník ABC a TRN
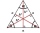 V rovnostranném trojúhelníku ABC je bod T jeho těžištěm, bod R je obrazem bodu T v osové souměrnosti podle přímky AB a bod N je obrazem bodu T v osové souměrnosti podle přímky BC. Určitě poměr obsahů trojúhelníků ABC a TRN.
V rovnostranném trojúhelníku ABC je bod T jeho těžištěm, bod R je obrazem bodu T v osové souměrnosti podle přímky AB a bod N je obrazem bodu T v osové souměrnosti podle přímky BC. Určitě poměr obsahů trojúhelníků ABC a TRN.
- V trojúhelníku 4
 V trojúhelníku ABC jsou velikosti úhlů alfa beta gama v poměru 0,4 :0,2 :0,9. Výpočitat jejich velikost.
V trojúhelníku ABC jsou velikosti úhlů alfa beta gama v poměru 0,4 :0,2 :0,9. Výpočitat jejich velikost. - Světlo
 Světlo prochází rozhraním mezi vzduchem a sklem s indexem lomu 1,5. Určete: a) úhel lomu, dopadá-li světlo na rozhraní ze vzduchu pod úhlem 40°. b) úhel lomu, dopadá-li světlo na rozhraní ze skla pod úhlem 40°. c) úhel dopadu, jestliže se světlo při dopad
Světlo prochází rozhraním mezi vzduchem a sklem s indexem lomu 1,5. Určete: a) úhel lomu, dopadá-li světlo na rozhraní ze vzduchu pod úhlem 40°. b) úhel lomu, dopadá-li světlo na rozhraní ze skla pod úhlem 40°. c) úhel dopadu, jestliže se světlo při dopad - Koule ve kuželi
 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
