Sádrový odlitek
Sádrový odlitek má tvar pravidelného čtyřbokého jehlanu. Plášť je tvořen čtyřmi rovnostrannými trojúhelníky se stranou 5 m. Vypočítejte objem a povrch.
Správná odpověď:
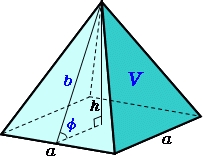
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - Obrazec
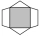 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu. - Dopravní 2
 Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí?
Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí? - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Pozemek 19
 Pozemek na stavbu rodinných domů má tvar pravoúhleho lichoběžníka se základnami délek 21m a 11,2m. Při ceně 2500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1352400 Kc. Jaká by byla délka pletiva potřebného k oplocení tohoto pozemku?
Pozemek na stavbu rodinných domů má tvar pravoúhleho lichoběžníka se základnami délek 21m a 11,2m. Při ceně 2500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1352400 Kc. Jaká by byla délka pletiva potřebného k oplocení tohoto pozemku? - Je dán 26
 Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem
Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem - Vypočítejte 82693
 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - Napište 3
 Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0.
Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0. - Rovnoběžníku 82626
 Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší.
Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší. - Žebřík 16
 Žebřík má délku 7 metrů a je opřen o zeď tak, že jeho dolní konec zdu je vzdálen 4 metry, Urči do jaké výšky dosahuje žebřík
Žebřík má délku 7 metrů a je opřen o zeď tak, že jeho dolní konec zdu je vzdálen 4 metry, Urči do jaké výšky dosahuje žebřík
