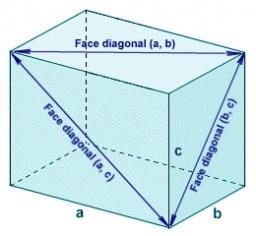
Poměr délky úhlopříček
Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček?
Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru.
Výsledek
Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru.
Výsledek
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Číslo 40
 Číslo 112 rozděl na tři složky x, y, z tak, aby platilo x : y = 7 : 5 a y : z = 3 : 4.
Číslo 112 rozděl na tři složky x, y, z tak, aby platilo x : y = 7 : 5 a y : z = 3 : 4. - Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Produkce
 Měsíční produkce podniku se zvýšila z 352 výrobků na 528 výrobků. O kolik procent tedy původní měsíční produkce vzrostla?
Měsíční produkce podniku se zvýšila z 352 výrobků na 528 výrobků. O kolik procent tedy původní měsíční produkce vzrostla? - Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Peleton
 Při cyklistických závodech jede peleton průměrnou rychlostí 36 km/h. Opravovou defektu se jeden závodník zdržel 5 minut. O kolik kilometrů za hodinu byla pak jeho rychlost větší než rychlost peletonu když ho dostihl za 20 minut? Jak dlouho by mu trvalo kd
Při cyklistických závodech jede peleton průměrnou rychlostí 36 km/h. Opravovou defektu se jeden závodník zdržel 5 minut. O kolik kilometrů za hodinu byla pak jeho rychlost větší než rychlost peletonu když ho dostihl za 20 minut? Jak dlouho by mu trvalo kd - Ovoce 7
 Cena 6 kg hrušek je o 77 Kč vyšší než cena 5 kg jablek. Cena 6 kg jablek je stejná jako cena 5 kg hrušek. Kolik stojí 2 kg jablek?
Cena 6 kg hrušek je o 77 Kč vyšší než cena 5 kg jablek. Cena 6 kg jablek je stejná jako cena 5 kg hrušek. Kolik stojí 2 kg jablek? - Evelína 2
 Evelína zryje zahradu za 4 hodiny. Její kamarádka Doubravka to zvládne za tři hodiny. Evelína začala pracovat ve 13 hodin a hodinu později se k ní přidala Doubravka, aby se spolu mohly jít koupat. Vypočítejte, v kolik hodin budou moci dívky odejít na koup
Evelína zryje zahradu za 4 hodiny. Její kamarádka Doubravka to zvládne za tři hodiny. Evelína začala pracovat ve 13 hodin a hodinu později se k ní přidala Doubravka, aby se spolu mohly jít koupat. Vypočítejte, v kolik hodin budou moci dívky odejít na koup - Známky 5
 Známky se stejnou vahou 2,1,3,2,2,3,1,3,1,1,2,4,2,2,3,1,1,2,1,3 urči: 1) aritmetický průměr 2) absolutní a relativní četnost 3) modus a medián 4) vytvoř graf
Známky se stejnou vahou 2,1,3,2,2,3,1,3,1,1,2,4,2,2,3,1,1,2,1,3 urči: 1) aritmetický průměr 2) absolutní a relativní četnost 3) modus a medián 4) vytvoř graf - Vykrátiť 2
 Vyhodnotťe nasledovný výraz s faktoriálmi: (45!-44!)/(44!)
Vyhodnotťe nasledovný výraz s faktoriálmi: (45!-44!)/(44!) - Krize
 Firma během krize propouštěla zaměstnance, takže jich měla na konci krize o 40 % méně než před krizí. Když firma po odeznění krize přijala 42 nových zaměstnanců, měla jich o 25 % více než na konci krize. Kolik zaměstnanců měla firma před krizí?
Firma během krize propouštěla zaměstnance, takže jich měla na konci krize o 40 % méně než před krizí. Když firma po odeznění krize přijala 42 nových zaměstnanců, měla jich o 25 % více než na konci krize. Kolik zaměstnanců měla firma před krizí? - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH. - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku. - Košíkář
 Košíkář prodal během prvních dvou dnů velikonoční trhu všechny upletene pomlazky, první den prodal pětinu všech pomlázek. Druhy den prodal o 180 pomlazek více než první den. Kolik pomlazek prodal kosikar první den velikonočních trhu?
Košíkář prodal během prvních dvou dnů velikonoční trhu všechny upletene pomlazky, první den prodal pětinu všech pomlázek. Druhy den prodal o 180 pomlazek více než první den. Kolik pomlazek prodal kosikar první den velikonočních trhu? - Plán dnes
 Traktorista má plán zorat 24 ha pole. Zoral již 20,64 ha. Na kolik procent již splnil plán?
Traktorista má plán zorat 24 ha pole. Zoral již 20,64 ha. Na kolik procent již splnil plán? - V koloně
 V koloně před mýtnou bránou stojí osobní auta a nákladní auta. Nákladní vůz je třikrát delší než osobní auto. Vypočítej, kolik stojí před autem, které právě přijelo, osobních aut, když je mezi nimi i jeden nákladní vůz, který tvoří jednu osminu délky fron
V koloně před mýtnou bránou stojí osobní auta a nákladní auta. Nákladní vůz je třikrát delší než osobní auto. Vypočítej, kolik stojí před autem, které právě přijelo, osobních aut, když je mezi nimi i jeden nákladní vůz, který tvoří jednu osminu délky fron
