Šetření po centoch
První den si odložím 1 cent a každý další o cent víc.
Kolik si naspořit za rok (365 dní)?
Kolik si naspořit za rok (365 dní)?
Správná odpověď:

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Trojúhelníkový 81985
 Cvičenci stojí na značkách v řadách vzdálených od sebe přesně 1,5m. Tvoří rozšiřující se trojúhelníkový klín (v každé následující řadě je o jednoho cvičence více), přičemž vzdálenost čelního cvičence od zadní řady je 30m. Určete počet cvičenců.
Cvičenci stojí na značkách v řadách vzdálených od sebe přesně 1,5m. Tvoří rozšiřující se trojúhelníkový klín (v každé následující řadě je o jednoho cvičence více), přičemž vzdálenost čelního cvičence od zadní řady je 30m. Určete počet cvičenců. - Posloupnosti 60183
 Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: n = 4, an = 12,5, sn = 187,5, a1=?, q=?
Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: n = 4, an = 12,5, sn = 187,5, a1=?, q=? - 1!+2!+3!+ 34441
 Najděte zbytek po dělení, když dělíme součet 1!+2!+3!+. .. . . +300! číslem 13.
Najděte zbytek po dělení, když dělíme součet 1!+2!+3!+. .. . . +300! číslem 13. - Součet obsahů
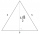 Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
- V množině
 V množině N řešte danou rovnici: 1 – x + x² - x³ + x4 – x5 + …. + = 1/3
V množině N řešte danou rovnici: 1 – x + x² - x³ + x4 – x5 + …. + = 1/3 - 1/3+1/9+1/27+1/81 4113
 Určete součet nekonečné řady: 1/3+1/9+1/27+1/81.. .
Určete součet nekonečné řady: 1/3+1/9+1/27+1/81.. . - Zázračný strom
 Zázračný strom roste tak rychle, že se první den zvětší jeho výška o polovinu celkové výšky, druhý den o třetinu, třetí den o čtvrtinu, atd. Kolikrát se zvětší jeho výška za 6 dní?
Zázračný strom roste tak rychle, že se první den zvětší jeho výška o polovinu celkové výšky, druhý den o třetinu, třetí den o čtvrtinu, atd. Kolikrát se zvětší jeho výška za 6 dní? - Desetinné číslo
 Zapište zlomkem A / B v základním tvaru desetinné číslo 6,015111111... (t.j. s nekonečným desetinným rozvojem).
Zapište zlomkem A / B v základním tvaru desetinné číslo 6,015111111... (t.j. s nekonečným desetinným rozvojem). - Zlomek
 Číslo frac(0, overline(75))(0,75) zapište jako zlomek a/b, kde a je čitatel a b jmenovatel. a, b = přirozená čísla.
Číslo frac(0, overline(75))(0,75) zapište jako zlomek a/b, kde a je čitatel a b jmenovatel. a, b = přirozená čísla.
- Rekurze čtverce
 Do čtverce ABCD je vepsán čtverec tak, že jeho vrcholy leží ve středech stran čtverce ABCD. Tomu je vepsán čtverec stejným způsobem. Postup se opakuje. Délka strany čtverce ABCD je a=37 cm. Jak velký je: a) součet obvodů všech čtverců, b) součet obsahů ?
Do čtverce ABCD je vepsán čtverec tak, že jeho vrcholy leží ve středech stran čtverce ABCD. Tomu je vepsán čtverec stejným způsobem. Postup se opakuje. Délka strany čtverce ABCD je a=37 cm. Jak velký je: a) součet obvodů všech čtverců, b) součet obsahů ? - Pracovníci 4
 Pracovníci jedné dílny obráběli během tří měsíců stejné součástky. Jejich výkon stoupal tak, že každý následující měsíc obrobili o 10 procent více součástek než v předcházejícím měsíci. V posledním měsíci obrobili 484 součástek. Kolik součástek obrobili v
Pracovníci jedné dílny obráběli během tří měsíců stejné součástky. Jejich výkon stoupal tak, že každý následující měsíc obrobili o 10 procent více součástek než v předcházejícím měsíci. V posledním měsíci obrobili 484 součástek. Kolik součástek obrobili v - Výsledky
 Výsledky osmých tříd z testu: 8D =? 8B = 47 8A = 44 8E = 37 8C = 28 Přesně průměrného výsledku dosáhla třída 8A. Kolik bodů získala vítězná třída 8D? O kolik % je úspěšnější třída 8B než 8C?
Výsledky osmých tříd z testu: 8D =? 8B = 47 8A = 44 8E = 37 8C = 28 Přesně průměrného výsledku dosáhla třída 8A. Kolik bodů získala vítězná třída 8D? O kolik % je úspěšnější třída 8B než 8C? - Zatáčka 3
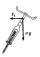 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Pokémony
 Jenda, Milan a Tomáš mají dohromady 203 kartiček s Pokémony. Jenda má dvakrát více kartiček než Tomáš. Milan má čtvrtinu z Jendova počtu kartiček. a) Kolik kartiček má Jenda? b) O kolik kartiček méně má Milan než Jenda s Tomášem dohromady?
Jenda, Milan a Tomáš mají dohromady 203 kartiček s Pokémony. Jenda má dvakrát více kartiček než Tomáš. Milan má čtvrtinu z Jendova počtu kartiček. a) Kolik kartiček má Jenda? b) O kolik kartiček méně má Milan než Jenda s Tomášem dohromady?
- Autobus 27
 Autobus vyjel z Prahy ve 20h45min a do Popradu přijel v 5h35min, jak dlouho jel autobus?
Autobus vyjel z Prahy ve 20h45min a do Popradu přijel v 5h35min, jak dlouho jel autobus? - Dekadické číslo rozvoj
 Jaký je rozšířený tvar tohoto čísla? 18,029 A: (1x10)+(8x1)+(2x1/10)+(9x1/100) B: (1×10)+(8×1)+(2×1/10)+(9×1/1000) C: (1×10)+(8×1)+(2×1/100)+(9×1/1000) D: (1×10)+(8×1)+(2×11/00)+(9×1/100)
Jaký je rozšířený tvar tohoto čísla? 18,029 A: (1x10)+(8x1)+(2x1/10)+(9x1/100) B: (1×10)+(8×1)+(2×1/10)+(9×1/1000) C: (1×10)+(8×1)+(2×1/100)+(9×1/1000) D: (1×10)+(8×1)+(2×11/00)+(9×1/100) - Do kroužku
 Do kroužku chodí 29 dětí. 11 uvedlo, že má doma psa, 14 dětí má doma kočku a 12 dětí má doma křečka. Dvě děti mají všechna tři zvířátka. 7 dětí nemá doma žádné zvíře. . Kolik dětí má alespoň dvě z uvedených zvířat? Kolik dětí má právě jedno z uvedených zv
Do kroužku chodí 29 dětí. 11 uvedlo, že má doma psa, 14 dětí má doma kočku a 12 dětí má doma křečka. Dvě děti mají všechna tři zvířátka. 7 dětí nemá doma žádné zvíře. . Kolik dětí má alespoň dvě z uvedených zvířat? Kolik dětí má právě jedno z uvedených zv
