Trojboký jehlan
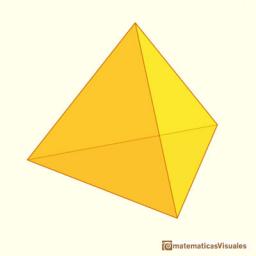
Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm.
Správná odpověď:
Zobrazuji 4 komentáře:
Petr
nahodou neni, kedze vyska ihlanu je delka hrany podstavy. Cize tie bocne hrany su dlhsie ako hrany podstavy
Zs Ucitel
3b jehlan: 4 vrcholy a 6 hran , 3 steny, 1 podstava
4b jehlan: 5 vrcholy a 8 hran , 4 steny, 1 podstava
4b jehlan: 5 vrcholy a 8 hran , 4 steny, 1 podstava
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- aritmetika
- odmocnina
- stereometrie
- jehlan
- povrch tělesa
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obsah
- trojúhelník
- čísla
- zlomky
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Hranol RRPT
 Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm.
Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm. - Kužel
 Kužel měří na základně průměr 6 palců. Vzdálenost od okraje obvodu k vrcholu je 12 palců. Najděte jeho objem. (palec=inch)
Kužel měří na základně průměr 6 palců. Vzdálenost od okraje obvodu k vrcholu je 12 palců. Najděte jeho objem. (palec=inch) - Urči poloměr RS kužela
 Urči poloměr a výšku (v centimetrech) rovnostranného kúželu, který má objem 1 litr
Urči poloměr a výšku (v centimetrech) rovnostranného kúželu, který má objem 1 litr - Vypočítejte
 Vypočítejte hmotnost dřevěného pravidelného trojbokého hranolu s výškou rovnající se obvodu podstavy a postavou vepsanou do kružnice o poloměru 6, M cm, kde M je měsíc vašeho narození. Hustota dubu je 680 kg/m³.
Vypočítejte hmotnost dřevěného pravidelného trojbokého hranolu s výškou rovnající se obvodu podstavy a postavou vepsanou do kružnice o poloměru 6, M cm, kde M je měsíc vašeho narození. Hustota dubu je 680 kg/m³. - 3S hranol
 Najděte objem a povrch trojúhelníkového hranolu s pravoúhlým trojúhelníkovým dnem, pokud je délka odvěsen dna hranolu je 7,2 cm a 4,7 cm a výška hranolu je 24 cm.
Najděte objem a povrch trojúhelníkového hranolu s pravoúhlým trojúhelníkovým dnem, pokud je délka odvěsen dna hranolu je 7,2 cm a 4,7 cm a výška hranolu je 24 cm. - Čtvercovou 44061
 Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška.
Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška. - Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH. - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku. - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm. - Obrazec
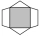 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Užitím 2
 Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α.
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
