Vypočítejte 30
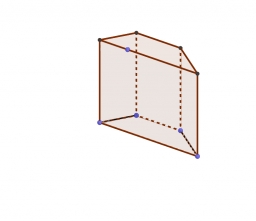
Vypočítejte objem čtyřbokého hranolu, který má podstavu rovnoramenného lichoběžníku se základnami 10 cm a 4 cm, vzdálených od sebe 6 cm . Výška hranolu je 25 cm . Můžeš se zamyslet, jak by bylo možné vypočítat povrch?
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- aritmetika
- odmocnina
- stereometrie
- povrch tělesa
- hranol
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obsah
- obvod
- lichoběžník
- obdélník
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH. - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
- Máme vodu
 Máme vodu 67°C 160 L, Kolik litrů studené vody 18°C na ochlazení na 39°C?
Máme vodu 67°C 160 L, Kolik litrů studené vody 18°C na ochlazení na 39°C? - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm. - V zeleném
 V zeleném kanystru bylo ráno o 6 litrů více než v modrém. Odpoledne zahradník 1 litr vody ze zeleného kanystru do modrého. v zeleném kanystru pak bylo dvakrát více vody než v modrém. Kolik bylo ráno v zeleném kanystru. Kolik bylo v obou dohromady.
V zeleném kanystru bylo ráno o 6 litrů více než v modrém. Odpoledne zahradník 1 litr vody ze zeleného kanystru do modrého. v zeleném kanystru pak bylo dvakrát více vody než v modrém. Kolik bylo ráno v zeleném kanystru. Kolik bylo v obou dohromady. - Katka 7
 Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá
Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá - Chemické výpočty
 50% roztok soli je třeba naředit destilovanou vodou tak, aby vzniklo 20 litrů 35% roztoku. Kolik litrů původního roztoku a kolik litrů vody potřebujeme?
50% roztok soli je třeba naředit destilovanou vodou tak, aby vzniklo 20 litrů 35% roztoku. Kolik litrů původního roztoku a kolik litrů vody potřebujeme?
- Sud, kbelík, konvička
 Vnitřní objem sudu je 15krát větší než objem kbelíku. Objem kbelíku je 5krát větší než objem konvičky. Ze sudu plného vody jsme třetinu vody odebrali, takže v něm zbylo 60 litrů vody. Vypočtěte v litrech objem konvičky.
Vnitřní objem sudu je 15krát větší než objem kbelíku. Objem kbelíku je 5krát větší než objem konvičky. Ze sudu plného vody jsme třetinu vody odebrali, takže v něm zbylo 60 litrů vody. Vypočtěte v litrech objem konvičky. - Kuchyňský
 Kuchyňský ocet je 8% roztok kyseliny octové ve vodě. Kolik litrů kyseliny octové je třeba na výrobu 275 l octa?
Kuchyňský ocet je 8% roztok kyseliny octové ve vodě. Kolik litrů kyseliny octové je třeba na výrobu 275 l octa? - Morská vs sladká
 Nákladní člun o celkové hmotnosti 4500t připlul z řeky do moře. Vypočtěte, o kolik tun je možno zvětšit hmotnost nákladu na člunu na moři, aby ponor zůstal stejný jako v řece. Hustota říční vody je 998 kg/m³. Hustota mořské vody je 1031 kg/m³. Príklad na
Nákladní člun o celkové hmotnosti 4500t připlul z řeky do moře. Vypočtěte, o kolik tun je možno zvětšit hmotnost nákladu na člunu na moři, aby ponor zůstal stejný jako v řece. Hustota říční vody je 998 kg/m³. Hustota mořské vody je 1031 kg/m³. Príklad na - Nádrž 32
 Nádrž se naplní jedním přítokem za 30 minut, druhým za 24 minut. Za kolik minut se naplní, jsou-li otevřeny oba průtoky současně.
Nádrž se naplní jedním přítokem za 30 minut, druhým za 24 minut. Za kolik minut se naplní, jsou-li otevřeny oba průtoky současně. - Nádrž 31
 Nádrž o objemu 15 hl má dva přítoky. Jedním přitéká 5 litrů za minutu, druhým 3 litry za minutu. Za jakou dobu se nádrž naplní oběma přítoky současně?
Nádrž o objemu 15 hl má dva přítoky. Jedním přitéká 5 litrů za minutu, druhým 3 litry za minutu. Za jakou dobu se nádrž naplní oběma přítoky současně?
- Jaké množství
 Jaké množství betonu je třeba objednat pro vybetonování rodinného domu obdélníkového půdorysu o rozměrech 15 m × 12,6 m při použití ztraceného bednění. Hloubka základů tvořený ztracenými bedněním je stanovena na 80cm. Použitý beton tvoří 80% objemu tvárni
Jaké množství betonu je třeba objednat pro vybetonování rodinného domu obdélníkového půdorysu o rozměrech 15 m × 12,6 m při použití ztraceného bednění. Hloubka základů tvořený ztracenými bedněním je stanovena na 80cm. Použitý beton tvoří 80% objemu tvárni - Mějme
 Mějme kostku jejíž délka hrany vyjádřená v centimetrech je přirozené číslo. Z jakého nejmenšího počtu takových stejných kostek lze vytvořit kvádr o rozměrech 24cm, 32cm a 60 cm. Jak dlouhá bude hrana těchto kostek?
Mějme kostku jejíž délka hrany vyjádřená v centimetrech je přirozené číslo. Z jakého nejmenšího počtu takových stejných kostek lze vytvořit kvádr o rozměrech 24cm, 32cm a 60 cm. Jak dlouhá bude hrana těchto kostek? - Sestavte
 Sestavte 3D model čtyřbokého jehlanu s podstavou obdélníku a stěnami rovnoramennými trojúhelníky, přičemž objem je 80 cm krychlových. Potřebovala bych znát strany a výšku.
Sestavte 3D model čtyřbokého jehlanu s podstavou obdélníku a stěnami rovnoramennými trojúhelníky, přičemž objem je 80 cm krychlových. Potřebovala bych znát strany a výšku.
