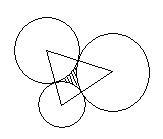
Vnější dotyk
Sestrojte kružnice k1 ( S1; 1,5 cm), k2 ( S2 ; 2 cm) a k3 ( S3 ; 2,5 cm ), tak aby měly vždy dvě vnější dotyk. Vypočtěte obvod trojúhelníka S1S2S3.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku. - Obrazec
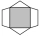 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Užitím 2
 Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α.
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu. - Dopravní 2
 Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí?
Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí? - Vypočítejte 82693
 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Rovnoběžníku 82626
 Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší.
Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší. - Čtyřúhulník AFHD
 Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD.
Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD. - Rs3 hranol
 Vypočtěte objem a povrch hranolu o výšce 9,6 cm s podstavou rovnostranného trojúhelníka o straně délky 4,8 cm.
Vypočtěte objem a povrch hranolu o výšce 9,6 cm s podstavou rovnostranného trojúhelníka o straně délky 4,8 cm. - Tramvajová úloha
 Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15. - Určete 49
 Určete bod C tak, aby trojúhelník ABC byl pravoúhlý a rovnoramenný s přeponou AB, kde A[4,-6], B[-2,10]
Určete bod C tak, aby trojúhelník ABC byl pravoúhlý a rovnoramenný s přeponou AB, kde A[4,-6], B[-2,10]
