Povrch a objem
Vypočítejte povrch a objem rotačního kužele, jestliže obvod jeho podstavy je 62,8 m a strana má délku 25 m.
Správná odpověď:
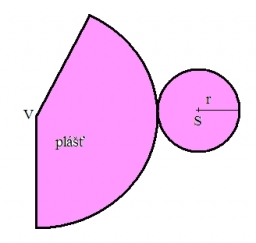
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- stereometrie
- kužel
- povrch tělesa
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- kruh, kružnice
- obvod
- trojúhelník
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - Plášť válce 3
 Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm. Jaký je povrch válce?
Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm. Jaký je povrch válce? - Je dán 26
 Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem
Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem - Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - 1 kg cukru
 1 kg kostkového cukru je tvořeno 840 krychlička o hraně 1,1 cm. Určete hustotu cukru a rozměr krabice jsou-li krychličky narovnány v sedmi řadách po devíti kostičkách. Kolik čtverečních metrů kartónu je třeba na výrobu 3000 těchto krabic?
1 kg kostkového cukru je tvořeno 840 krychlička o hraně 1,1 cm. Určete hustotu cukru a rozměr krabice jsou-li krychličky narovnány v sedmi řadách po devíti kostičkách. Kolik čtverečních metrů kartónu je třeba na výrobu 3000 těchto krabic? - Rs3 hranol
 Vypočtěte objem a povrch hranolu o výšce 9,6 cm s podstavou rovnostranného trojúhelníka o straně délky 4,8 cm.
Vypočtěte objem a povrch hranolu o výšce 9,6 cm s podstavou rovnostranného trojúhelníka o straně délky 4,8 cm. - Válec 28
 Válec má povrch pláště 88 cm čtverečních a objem 176 cm krychlových. Vypočítejte poloměr, výšku a povrch uvedeného tělesa
Válec má povrch pláště 88 cm čtverečních a objem 176 cm krychlových. Vypočítejte poloměr, výšku a povrch uvedeného tělesa - Stínítko
 Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem
Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Objem 32
 Objem krychle je 0,512 m³. Vypočtěte její povrch.
Objem krychle je 0,512 m³. Vypočtěte její povrch. - Vypočítej 393
 Vypočítej objem a povrch kužele s průměrem podstavy d = 22 cm a tělesovou výškou v = 40 cm
Vypočítej objem a povrch kužele s průměrem podstavy d = 22 cm a tělesovou výškou v = 40 cm - Do koule
 Do koule o poloměru 27 cm je vepsána krychle. Vypočtěte její objem a povrch.
Do koule o poloměru 27 cm je vepsána krychle. Vypočtěte její objem a povrch. - Povrch 33
 Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru.
Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru. - Vypočtěte 26
 Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm.
Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm. - Objem 31
 Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru. - Objem 30
 Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru. - Truhlář 5
 Truhlář opracovával rotační válec s poloměrem podstavy 2,5dm a výškou 2dm. Rovnoměrným broušením zmenšil poloměr o 1cm, výška válce byla zachována. Vypocitej, o kolik procent se zmenšil obsah válce.
Truhlář opracovával rotační válec s poloměrem podstavy 2,5dm a výškou 2dm. Rovnoměrným broušením zmenšil poloměr o 1cm, výška válce byla zachována. Vypocitej, o kolik procent se zmenšil obsah válce.
