Jama 3
Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m3 zeminy bylov ykopano při hloubení jámy?
Správná odpověď:
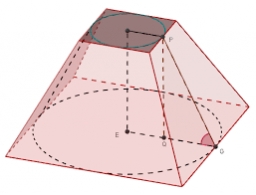
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- stereometrie
- jehlan
- komolý jehlan a kužel
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- čtverec
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku. - Užitím 2
 Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α.
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu. - Dopravní 2
 Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí?
Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí? - Vypočítejte 82693
 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Tramvajová úloha
 Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15. - Minutová 9
 Minutová ručička opíše za půl hodiny úhel 180 stupňů. Za kolik minut opíše minutová ručička úhel o velikosti 192 stupňů?
Minutová ručička opíše za půl hodiny úhel 180 stupňů. Za kolik minut opíše minutová ručička úhel o velikosti 192 stupňů? - Vypočítej 400
 Vypočítej vnitřní úhly trojúhelníku. Úhel alfa je o 16° větší než beta a úhel gama je o 17° menší než alfa.
Vypočítej vnitřní úhly trojúhelníku. Úhel alfa je o 16° větší než beta a úhel gama je o 17° menší než alfa. - Určete 48
 Určete rozdíl úhlových rychlostí hodinových ručiček. [rad/s] ω hodinových ručiček =? ω minutových ručiček =? ω sekundových ručiček =?
Určete rozdíl úhlových rychlostí hodinových ručiček. [rad/s] ω hodinových ručiček =? ω minutových ručiček =? ω sekundových ručiček =? - Kruhová 4
 Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr?
Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr? - Těžnice 10
 Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°.
Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°. - Tyč je
 Tyč je svisle zabodnuta do země. Vyčnívající délka je 1m. Jaká je délka vrženého stínu, když je slunce právě 50° nad horizontem?
Tyč je svisle zabodnuta do země. Vyčnívající délka je 1m. Jaká je délka vrženého stínu, když je slunce právě 50° nad horizontem?
