Čoko pyramída
Kolik čokolády je v 3. regálu, pokud v 8. regálu je 41 čokolád a v každém dalším regálu je o 7 čokolád více než v předchozím regálu.
Správná odpověď:

Zobrazuji 1 komentář:
Žák
Řešení je sice po dosazení do vzorce správné, nicméně logicky nedává smysl. Je totiž nemožné, aby v prvním regálu bylo -8 čokolád. Většina řešitelů totiž považuje 1. regál za nejvrchnější, ale v tomto případě by měl být nejspodnější a naopak 8. regál by měl být nejvrchnější. Vámi vyřešená posloupnost vypadá následovně: -8;-1;6;13;20;27;34;41, ale myslím si, že posloupnost vycházející z reálné situace by měla vypadat následovně: 41;48;55;62;69;76;83;90 a odpověď by tedy zněla, že ve třetím regále je 76 čokolád. Další možností je, že v prvním a druhém regálu vůbec žádná čokoláda není, ale to už by byla poněkud zvláštní Čoko pyramída:-) Budu velmi vděčný za Váš názor a přeji hezký zbytek dne.
S pozdravem
Daniel Čermák
S pozdravem
Daniel Čermák
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Pracovníci 4
 Pracovníci jedné dílny obráběli během tří měsíců stejné součástky. Jejich výkon stoupal tak, že každý následující měsíc obrobili o 10 procent více součástek než v předcházejícím měsíci. V posledním měsíci obrobili 484 součástek. Kolik součástek obrobili v
Pracovníci jedné dílny obráběli během tří měsíců stejné součástky. Jejich výkon stoupal tak, že každý následující měsíc obrobili o 10 procent více součástek než v předcházejícím měsíci. V posledním měsíci obrobili 484 součástek. Kolik součástek obrobili v - Do kroužku
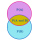
 Do kroužku chodí 29 dětí. 11 uvedlo, že má doma psa, 14 dětí má doma kočku a 12 dětí má doma křečka. Dvě děti mají všechna tři zvířátka. 7 dětí nemá doma žádné zvíře. . Kolik dětí má alespoň dvě z uvedených zvířat? Kolik dětí má právě jedno z uvedených zv
Do kroužku chodí 29 dětí. 11 uvedlo, že má doma psa, 14 dětí má doma kočku a 12 dětí má doma křečka. Dvě děti mají všechna tři zvířátka. 7 dětí nemá doma žádné zvíře. . Kolik dětí má alespoň dvě z uvedených zvířat? Kolik dětí má právě jedno z uvedených zv - Myslím 20
 Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím?
Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím? - Oddíl 6
 Oddíl má 90 členů. Starších dorostenců je v oddíle o 4 více než mladších dorostenců. Starších žáků je o 10 více než všech dorostenců. Kolik je v oddíle starších a mladších dorostenců a kolik starších žáků?
Oddíl má 90 členů. Starších dorostenců je v oddíle o 4 více než mladších dorostenců. Starších žáků je o 10 více než všech dorostenců. Kolik je v oddíle starších a mladších dorostenců a kolik starších žáků? - V obecném
 V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů.
V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů. - Každý 5
 Každý ze tří sčítanců je o 5 větší než předchozí. Součet všech je 78. O která čísla se jedná.
Každý ze tří sčítanců je o 5 větší než předchozí. Součet všech je 78. O která čísla se jedná. - Pravděpodobnost 63434
 V obálce jsou lístky s čísly 1, 2, 3, 4, 5, 6, 7, 8. Z obálky se vytahují vždy najednou dva lístky. Jaká je pravděpodobnost, že součet vytažených čísel bude 7? sledek zapište jako desetinné číslo zaokrouhlené na setiny. A) 0,21 B) 0,05 C) 0,22 D) 0,11
V obálce jsou lístky s čísly 1, 2, 3, 4, 5, 6, 7, 8. Z obálky se vytahují vždy najednou dva lístky. Jaká je pravděpodobnost, že součet vytažených čísel bude 7? sledek zapište jako desetinné číslo zaokrouhlené na setiny. A) 0,21 B) 0,05 C) 0,22 D) 0,11 - Červených 63284
 V balíčku jsou bílé, červené a zelené bonbóny. Počet bílých a červených bonbonů je v poměru 1:3, počet červených a zelených bonbonů je v poměru 4:7. Zelených bonbonů je o 20 více než bílých a červených dohromady. Kolik je všech bonbonů?
V balíčku jsou bílé, červené a zelené bonbóny. Počet bílých a červených bonbonů je v poměru 1:3, počet červených a zelených bonbonů je v poměru 4:7. Zelených bonbonů je o 20 více než bílých a červených dohromady. Kolik je všech bonbonů? - Po vodorovné
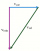 Po vodorovné trati jede auto stálou rychlostí 20 m∙s–1. Prší. Kapky deště padají ve svislém směru rychlostí o velikosti 6 m∙s–1. a) Jak velká je rychlost kapek vzhledem k oknům auta? b) Jaký úhel svírají stopy dešťových kapek na okně auta se svislým směre
Po vodorovné trati jede auto stálou rychlostí 20 m∙s–1. Prší. Kapky deště padají ve svislém směru rychlostí o velikosti 6 m∙s–1. a) Jak velká je rychlost kapek vzhledem k oknům auta? b) Jaký úhel svírají stopy dešťových kapek na okně auta se svislým směre - Součet 36
 Součet dvou čísel je 69 a rozdíl 11. Která čísla to jsou?
Součet dvou čísel je 69 a rozdíl 11. Která čísla to jsou? - Třemi kostkami
 Jaká je pravděpodobnost, že při hodu třemi hracími kostkami (B, M, Z) bude součet teček 14?
Jaká je pravděpodobnost, že při hodu třemi hracími kostkami (B, M, Z) bude součet teček 14? - Sestavovala 58943
 Vírka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1554. Jaké číslice Vierka použila?
Vírka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1554. Jaké číslice Vierka použila? - 9 z 10 čísel
 Určete počet devítimístných čísel, ve kterých se každá z číslic 0 až 9 vyskytuje nejvíce jednou a v nichž se součty číslic na 1. až 3. místě, na 3. až 5. místě, na 5. až 7. místě a na 7. až 9. místě vždy rovnají 10. Najděte i nejmenší a největší z těchto
Určete počet devítimístných čísel, ve kterých se každá z číslic 0 až 9 vyskytuje nejvíce jednou a v nichž se součty číslic na 1. až 3. místě, na 3. až 5. místě, na 5. až 7. místě a na 7. až 9. místě vždy rovnají 10. Najděte i nejmenší a největší z těchto - Na kružnici
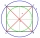 Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC.
Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC. - Rozdělit 54861
 Umíte číslo 64,9 rozdělit na tři sčítance tak, aby první s druhým byly v poměru 4:5 a třetí s prvním v poměru 7:3?
Umíte číslo 64,9 rozdělit na tři sčítance tak, aby první s druhým byly v poměru 4:5 a třetí s prvním v poměru 7:3? - Knihkupec 2
 Kniha byla z 350 Kč zdražena o 20 %. Jelikož nešla na odbyt, zlevnil ji následně knihkupec o 15 %. Kolik byla její koncová cena?
Kniha byla z 350 Kč zdražena o 20 %. Jelikož nešla na odbyt, zlevnil ji následně knihkupec o 15 %. Kolik byla její koncová cena? - MATEMATIK: 46893
 Řešení úlohy, náhrad písmena ciframi ve slově MATEMATIK: MAT + EMA = TIK
Řešení úlohy, náhrad písmena ciframi ve slově MATEMATIK: MAT + EMA = TIK
