Koza
Ve čtvercové zahradě o straně (a), je uprostřed jedné strany uvázaná koza. Spočítej délku provazu (r) tak, aby koza spásla přesně půlku zahrady. Platí r=c*a, urči konstantu c.
Správná odpověď:
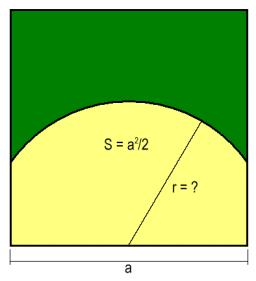
Zobrazuji 2 komentáře:
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- rovnice
- vyjádření neznámé ze vzorce
- planimetrie
- Pythagorova věta
- kruh, kružnice
- trojúhelník
- čtverec
- kruhová výseč
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Ortocentrum
 Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran.
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran. - Podstavy
 Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav.
Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav. - V Kocourkově 2
 V Kocourkově se rozhodli, že postaví dětské hřiště a volejbalové. Volejbalové bude mít rozměr 18m x 19m. Dětske hřiště bude mít tvář čtverce. Plocha obou hřišť bude stejná . Jaké budou rozměry dětského hřiště?
V Kocourkově se rozhodli, že postaví dětské hřiště a volejbalové. Volejbalové bude mít rozměr 18m x 19m. Dětske hřiště bude mít tvář čtverce. Plocha obou hřišť bude stejná . Jaké budou rozměry dětského hřiště? - Květinová
 Květinová zahrada má tvar čtverce. Nová zahrada má tvar obdélníku a její jeden rozměr je o 8 m menší a druhý je dvojnásobně větší než ve čtvercové zahradě. Jaké rozměry měla původní zahrada i nová zahrada, jestliže výměra obou zahrad je stejná?
Květinová zahrada má tvar čtverce. Nová zahrada má tvar obdélníku a její jeden rozměr je o 8 m menší a druhý je dvojnásobně větší než ve čtvercové zahradě. Jaké rozměry měla původní zahrada i nová zahrada, jestliže výměra obou zahrad je stejná?
- K MDŽ
 Srdce maminkám k MDŽ snadno vyrobíme tak, že ke dvěma horním stranám čtverce stojícím na svém vrcholu přikreslíme dva půlkruhy. Jaký poloměr bude mít kružnice opsaná tomuto srdci, když délka strany čtverce je rovna 1?
Srdce maminkám k MDŽ snadno vyrobíme tak, že ke dvěma horním stranám čtverce stojícím na svém vrcholu přikreslíme dva půlkruhy. Jaký poloměr bude mít kružnice opsaná tomuto srdci, když délka strany čtverce je rovna 1? - Je dána 5
 Je dána kružnice, do které je vepsán čtverec. Menší čtverec je vepsán do kruhové úseče tvořené stranou čtverce a obloukem dané kružnice. Jaký je poměr ploch velkého a malého čtverce?
Je dána kružnice, do které je vepsán čtverec. Menší čtverec je vepsán do kruhové úseče tvořené stranou čtverce a obloukem dané kružnice. Jaký je poměr ploch velkého a malého čtverce? - Čtverec ABCD
 Je dán čtverec ABCD s délkou strany 100 mm. Vypočítej poloměr kružnice, která prochází vrcholy B, C a středem strany AD.
Je dán čtverec ABCD s délkou strany 100 mm. Vypočítej poloměr kružnice, která prochází vrcholy B, C a středem strany AD. - Zvětšime-li
 Zvětšime-li délku jedné dvojice protilehlých stran čtverce o 2 cm a délku dalších dvou stran o 1cm vznikne obdélník, jehož obvod bude o 10% větší než obvod původního čtverce. Jaká je délka strany tohoto čtverce?
Zvětšime-li délku jedné dvojice protilehlých stran čtverce o 2 cm a délku dalších dvou stran o 1cm vznikne obdélník, jehož obvod bude o 10% větší než obvod původního čtverce. Jaká je délka strany tohoto čtverce? - Strana čtverce 3
 Jestliže stranu čtverce zvětšíme o třetinu, bude jeho obvod větší o 20 cm než původní. Jaká je strana čtverce?
Jestliže stranu čtverce zvětšíme o třetinu, bude jeho obvod větší o 20 cm než původní. Jaká je strana čtverce?
- Čtvercovou 19543
 Vypočítej povrch hranolu se čtvercovou podstavou jehož plášt je obdélník se stranami 18cm a 8cm. Kolik řešení má úkol? Uveďte všechna řešení.
Vypočítej povrch hranolu se čtvercovou podstavou jehož plášt je obdélník se stranami 18cm a 8cm. Kolik řešení má úkol? Uveďte všechna řešení. - Jestliže 2
 Jestliže stranu čtverce zvětšíme o polovinu, bude jeho obvod o 24 cm větší než původní. Jaká je strana čtverce?
Jestliže stranu čtverce zvětšíme o polovinu, bude jeho obvod o 24 cm větší než původní. Jaká je strana čtverce? - Délka úseku úsečky
 Předpokládejme, že víte, že délka úseku úsečky je 15, x2 = 6, y2 = 14 a x1 = -3. Najděte možnou hodnotu y1. Existuje více než jedna možná odpověď? Proč ano nebo proč ne?
Předpokládejme, že víte, že délka úseku úsečky je 15, x2 = 6, y2 = 14 a x1 = -3. Najděte možnou hodnotu y1. Existuje více než jedna možná odpověď? Proč ano nebo proč ne? - Nevybarvená 14513
 Čtverec abcd, je složen z 36 malých čtverců. 6 z nich jsou vybarveny. Kolik malých čtverců potřebujeme ještě vybarvit, aby čtvrtina plochy čtverce abcd zůstala nevybarvená?
Čtverec abcd, je složen z 36 malých čtverců. 6 z nich jsou vybarveny. Kolik malých čtverců potřebujeme ještě vybarvit, aby čtvrtina plochy čtverce abcd zůstala nevybarvená? - Zmenší-li
 Zmenší-li se délka stany čtvercové podložky o 6 cm, zmenší se její obsah o 2,76 dm². Urči délku strany původní i zmenšené podložky.
Zmenší-li se délka stany čtvercové podložky o 6 cm, zmenší se její obsah o 2,76 dm². Urči délku strany původní i zmenšené podložky.
- Obdélníkové 8136
 Rozdělte čtvercovou zahradu s obvodem 124 m na dvě obdélníkové zahrady tak, aby plot jedné zahrady byl o 10 m delší než plot druhé zahrady. Jaké rozměry budou mít tyto obdélníkové zahrady?
Rozdělte čtvercovou zahradu s obvodem 124 m na dvě obdélníkové zahrady tak, aby plot jedné zahrady byl o 10 m delší než plot druhé zahrady. Jaké rozměry budou mít tyto obdélníkové zahrady? - Obdélníku 8134
 Obvod obdélníku který lze rozdělit na 3 čtverce je 168 cm. Určete délky jeho stran.
Obvod obdélníku který lze rozdělit na 3 čtverce je 168 cm. Určete délky jeho stran. - V daném
 V daném obdélníku je délka o 12 m větší než šířka. Zmenšíme-li délku o 10 m a šířku zvětšíme o 2 m dostaneme čtverec. Plošný obsah původního obdélníku je o 300 m² větší než plošný obsah čtverce. Určete rozměry obdélníku.
V daném obdélníku je délka o 12 m větší než šířka. Zmenšíme-li délku o 10 m a šířku zvětšíme o 2 m dostaneme čtverec. Plošný obsah původního obdélníku je o 300 m² větší než plošný obsah čtverce. Určete rozměry obdélníku.
