Pětiúhelník
Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20.
Správná odpověď:

Zobrazuji 3 komentáře:
Žák
Úhlopříčka je úsečka, která spojuje dva různé nesousední vrcholy mnohoúhelníka. S = 237,24 (jednotka na druhou) :-)
Žák
S = 79,5168 jednotek čtverečních je plocha pro délku úhlopříčky 11, špatně jsem opsal zadání. Uvedené řešení je správné.
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Čtyřúhulník AFHD
 Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD.
Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD. - Z vrcholů 2
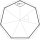 Z vrcholů pravidelného sedmiúhelníka vybereme náhodně trojici různých bodů a spojíme je úsečkami. Pravděpodobnost, že výsledný trojúhelník bude rovnoramenný, je rovna: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7
Z vrcholů pravidelného sedmiúhelníka vybereme náhodně trojici různých bodů a spojíme je úsečkami. Pravděpodobnost, že výsledný trojúhelník bude rovnoramenný, je rovna: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - Mnohoúhelníku 81152
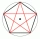 V jistém mnohoúhelníku platí, že poměr součtu velikosti jeho vnitřních úhlů a součtu velikosti k nim doplňkových úhlů je 2:5. Kolik vrcholů má tento mnohoúhelník?
V jistém mnohoúhelníku platí, že poměr součtu velikosti jeho vnitřních úhlů a součtu velikosti k nim doplňkových úhlů je 2:5. Kolik vrcholů má tento mnohoúhelník? - Čtyřúhelníku 66614
 Na obrázku je čtverec ABCD se středem S a stranou dlouhou 8 cm. Bod E je libovolný bod strany CD různé od C a D. Vypočítejte obsah čtyřúhelníku ASBE v cm².
Na obrázku je čtverec ABCD se středem S a stranou dlouhou 8 cm. Bod E je libovolný bod strany CD různé od C a D. Vypočítejte obsah čtyřúhelníku ASBE v cm². - Vypočítejte 196
 Vypočítejte objem a povrch pravidelného šestibokého hranolu o výšce v=2cm a podstavené hraně a=8cm.
Vypočítejte objem a povrch pravidelného šestibokého hranolu o výšce v=2cm a podstavené hraně a=8cm. - Pětiúhelník
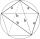 Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA
Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA - Podložka oktagon
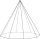 Potřebujete zhotovit podložku tvaru pravidelného osmiúhelníku o straně délky 4cm. Jaký minimální průměr by měl mít polotovar tvaru kruhu, ze kterého máme podložku zhotovit, a jaký pak bude odpad v procentech? (Výsledky zaokrouhlete na 1 desetinné místo)
Potřebujete zhotovit podložku tvaru pravidelného osmiúhelníku o straně délky 4cm. Jaký minimální průměr by měl mít polotovar tvaru kruhu, ze kterého máme podložku zhotovit, a jaký pak bude odpad v procentech? (Výsledky zaokrouhlete na 1 desetinné místo) - Koza
 Oplocený květinový záhon má tvar pravidelného šestiúhelníku, vrcholy tvoří sloupy plotu. Plot kolem záhonu měří 60 m. K jednomu ze sloupků je zvenku přivázána koza, která se pase na okolní louce (koza nemíchejte vejít do záhonu). Provázek měří 24 m. Kolik
Oplocený květinový záhon má tvar pravidelného šestiúhelníku, vrcholy tvoří sloupy plotu. Plot kolem záhonu měří 60 m. K jednomu ze sloupků je zvenku přivázána koza, která se pase na okolní louce (koza nemíchejte vejít do záhonu). Provázek měří 24 m. Kolik - Nepravidelný hexagon
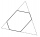 Je dán nepravidelný šestiúhelník, jehož strany jsou stejně dlouhé. Protilehlé strany jsou rovnoběžné a jejich vzdálenost činí 237 resp. 195 resp. 193. Jaká je jeho plocha?
Je dán nepravidelný šestiúhelník, jehož strany jsou stejně dlouhé. Protilehlé strany jsou rovnoběžné a jejich vzdálenost činí 237 resp. 195 resp. 193. Jaká je jeho plocha? - Kolik 80
 Kolik litrů vody se vejde do ozdobné zahradní nádržky tvaru pravidelného šestibokého jehlanu s hranou podstavy délky 30 cm? Hloubka nádržky je 30 cm.
Kolik litrů vody se vejde do ozdobné zahradní nádržky tvaru pravidelného šestibokého jehlanu s hranou podstavy délky 30 cm? Hloubka nádržky je 30 cm. - Vypočtěte 17
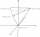 Vypočtěte povrch pravidelného čtyřstěnu, je-li délka stěnové výšky Vs=1 dm
Vypočtěte povrch pravidelného čtyřstěnu, je-li délka stěnové výšky Vs=1 dm - Rozmístěno 45573
 Na dětském kolotoči ve tvaru kružnice je rovnoměrně rozmístěno 5 sedaček. Jaké dlouhé je rameno kolotoče (spojující střed kolotoče se sedačkou), pokud vzdálenost mezi dvěma sedačkami je 1,2m.
Na dětském kolotoči ve tvaru kružnice je rovnoměrně rozmístěno 5 sedaček. Jaké dlouhé je rameno kolotoče (spojující střed kolotoče se sedačkou), pokud vzdálenost mezi dvěma sedačkami je 1,2m. - Rozmístěno 45471
 Na dětském kolotoči ve tvaru kružnice je rovnoměrně rozmístěno 12 sedaček. Jak dlouhé je rameno kolotoče (spojující střed kolotoče se sedačkou), pokud vzdálenost mezi dvěma sedačkami je 1,5m.
Na dětském kolotoči ve tvaru kružnice je rovnoměrně rozmístěno 12 sedaček. Jak dlouhé je rameno kolotoče (spojující střed kolotoče se sedačkou), pokud vzdálenost mezi dvěma sedačkami je 1,5m. - Slunečník
 Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%.
Slunečník má tvar pláště šestibokého pravidelného jehlanu, jehož podstavná hrana a=6dm a výška v=25cm. Kolik látky je třeba na zhotovení slunečníku, počítáme-li na spoje a odpad 10%. - Konvexní osmiúhleník
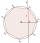 Do kružnice je vepsán nepravidelný konvexní osmiúhleník. Jeho 4 sousedící strany mají délku 3, zbylé 4 sousedící strany mají délku 2. Jaká je plocha daného osmiúhelníka?
Do kružnice je vepsán nepravidelný konvexní osmiúhleník. Jeho 4 sousedící strany mají délku 3, zbylé 4 sousedící strany mají délku 2. Jaká je plocha daného osmiúhelníka? - Šestiboký hranol
 Vypočtěte objem a povrch nádoby ve tvaru pravidelného šestibokého hranolu s výškou 1,4 m s hranou podstavy 3DM a příslušnou výškou 2,6 dm.
Vypočtěte objem a povrch nádoby ve tvaru pravidelného šestibokého hranolu s výškou 1,4 m s hranou podstavy 3DM a příslušnou výškou 2,6 dm. - Pravidelný 35781
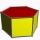 Pravidelný šestiboký hranol je vysoký 2 cm. Poloměr kružnice opsané podstavě je 8 cm. Určete jeho objem a povrch.
Pravidelný šestiboký hranol je vysoký 2 cm. Poloměr kružnice opsané podstavě je 8 cm. Určete jeho objem a povrch.
