Podobný trojúhelník
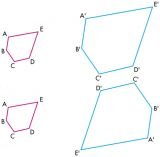
Strany trojúhelníku ABC mají délky 4 cm,5 cm a 7 cm. Sestroj trojúhelník A´B´C´ podobný trojúhelníku ABC, který má obvod 12 cm.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Sestroj 21
 Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek.
Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek. - Sestrojte 9
 Sestrojte lichoběžník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A velikost úhlu ABC=60°
Sestrojte lichoběžník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A velikost úhlu ABC=60° - Sestroj 19
 Sestroj pravoúhlý trojúhelník ABC s přeponou AB: a) |AB|=72 mm, |BC|=51 mm b) |AB|=58 mm, |AC|= 42 mm
Sestroj pravoúhlý trojúhelník ABC s přeponou AB: a) |AB|=72 mm, |BC|=51 mm b) |AB|=58 mm, |AC|= 42 mm - Rovnostranný 56651
 Rozdělte úsečku AB na tři stejné části. Návod: Sestrojte rovnostranný trojúhelník ABC a najděte jeho střed (např. popsané kružnice).
Rozdělte úsečku AB na tři stejné části. Návod: Sestrojte rovnostranný trojúhelník ABC a najděte jeho střed (např. popsané kružnice). - Vzdáleností 36831
 Je dána přímka p a dva vnitřní body jedné z polorovin, určených přímkou p. Najdi na přímce p bod X tak, aby součet jeho vzdáleností od bodů A, B byl nejmenší.
Je dána přímka p a dva vnitřní body jedné z polorovin, určených přímkou p. Najdi na přímce p bod X tak, aby součet jeho vzdáleností od bodů A, B byl nejmenší. - Redukčního 33021
 Narysuj úsečku AB=14 cm a rozdělte ji pomocí redukčního úhlu v poměru 2:9.
Narysuj úsečku AB=14 cm a rozdělte ji pomocí redukčního úhlu v poměru 2:9. - Konstrukce 32971
 Je dána libovolná kružnice k, která nemá vyznačený střed. Pomocí vhodné konstrukce najdi střed kružnice k. Vyzkoušej na 2 různých kružnicích.
Je dána libovolná kružnice k, která nemá vyznačený střed. Pomocí vhodné konstrukce najdi střed kružnice k. Vyzkoušej na 2 různých kružnicích. - Narysuj
 Narysuj lichoběžník, pokud b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Postup, diskuse, náčrt, rozbor, konstrukce)
Narysuj lichoběžník, pokud b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Postup, diskuse, náčrt, rozbor, konstrukce) - Menealovy 26771
 Ukažte (pomocí Menealovy věty), že těžiště dělí těžnici v poměru 1:2.
Ukažte (pomocí Menealovy věty), že těžiště dělí těžnici v poměru 1:2. - Konstrukční 13731
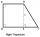 Mám pravoúhlý lichoběžník ZIMA (pravý úhel při vrcholu Z) ZI-7cm, ZM-5cm, AM-3,5cm a mám napsat i postup a provést zkoušku v konstrukční úloze
Mám pravoúhlý lichoběžník ZIMA (pravý úhel při vrcholu Z) ZI-7cm, ZM-5cm, AM-3,5cm a mám napsat i postup a provést zkoušku v konstrukční úloze - Trojúhelníku 7247
 Na straně AB trojúhelníku ABC jsou dány body D a E tak, že |AD| = |DE| = |EB|. Body A a B jsou postupně středy úseček CF a CG. Přímka CD protíná přímku FB v bodě I a přímka CE protíná přímku AG v bodě J. Dokažte, že průsečík přímek AI a BJ leží na přímce
Na straně AB trojúhelníku ABC jsou dány body D a E tak, že |AD| = |DE| = |EB|. Body A a B jsou postupně středy úseček CF a CG. Přímka CD protíná přímku FB v bodě I a přímka CE protíná přímku AG v bodě J. Dokažte, že průsečík přímek AI a BJ leží na přímce - Sestroj
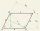 Sestroj rovnoběžník (kosodélník) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm.
Sestroj rovnoběžník (kosodélník) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm. - Úsečka 6
 Úsečka MN (/MN/ = 9cm) rozdělte na 11 stejných dílků
Úsečka MN (/MN/ = 9cm) rozdělte na 11 stejných dílků - Poloměrem 6500
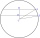 Narýsuj úsečku KL=55mm. Narýsuj kružnici k se středem K a poloměrem 4cm. Vyznačuj body tak, aby patřily kružnici a spojuj je s bodem L.
Narýsuj úsečku KL=55mm. Narýsuj kružnici k se středem K a poloměrem 4cm. Vyznačuj body tak, aby patřily kružnici a spojuj je s bodem L. - Rovnoramenný 6411
 Narýsuj rovnoramenný lichoběžník ABDC, pokud a=6cm, v=5cm, beta=60 stupňů. /náčrt, postup, konstrukce/
Narýsuj rovnoramenný lichoběžník ABDC, pokud a=6cm, v=5cm, beta=60 stupňů. /náčrt, postup, konstrukce/ - Dorýsuj
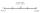 Dorýsuj úsečku AB, znáš-li jeden její krajní bod a střed úsečky S.
Dorýsuj úsečku AB, znáš-li jeden její krajní bod a střed úsečky S. - Zkonstruujte
 Zkonstruujte kosočtverec EFHG, kde e=6,7cm, výška na stranu h: v= fh =5cm
Zkonstruujte kosočtverec EFHG, kde e=6,7cm, výška na stranu h: v= fh =5cm
