Čtverec 23
Danův otec má doma čtverec z drátu o hmotnosti 65,25 miligramů, spolu s diagonální úhlopříčkou. Jak bude čtverec velký, když jeden mm váží 7 mg?
Správná odpověď:
Zobrazuji 2 komentáře:
Žák
Správně: a (mm) = o1/(4 + sqrt(2)) = 9,3214/(4 + sqrt(2)) = 1,7217 mm.
Lepší otázka: Čím je Danův otec?
Lepší otázka: Čím je Danův otec?
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Tip: Převody jednotky hustoty vám pomůže naše kalkulačka pro převody jednotek hustoty.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Chcete proměnit jednotku délky?
Tip: Převody jednotky hustoty vám pomůže naše kalkulačka pro převody jednotek hustoty.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obvod
- trojúhelník
- čtverec
- úhlopříčka
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Obrazec
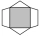 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Vypočítej 391
 Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm
Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm - Z7–I–5 MO 2022
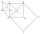 Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte...
Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte... - Mo z9 2022 čtverce
 Vrcholy čtverce ABCD spojuje lomená čára DEFGHB. Menší úhly u vrcholů E, F, G, H jsou pravé a úsečky DE, EF, FG, GH, HB po řadě měří 6 cm, 4cm, 4 cm, 1 cm, 2 cm. Určete obsah čtverce ABCD.
Vrcholy čtverce ABCD spojuje lomená čára DEFGHB. Menší úhly u vrcholů E, F, G, H jsou pravé a úsečky DE, EF, FG, GH, HB po řadě měří 6 cm, 4cm, 4 cm, 1 cm, 2 cm. Určete obsah čtverce ABCD. - Svislý
 Svislý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikne ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3cm a 4cm. Výška hranolu je 8 cm. Jaký je objem šestib
Svislý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikne ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3cm a 4cm. Výška hranolu je 8 cm. Jaký je objem šestib - Jak velká
 Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo.
Jak velká je hnědě vybarvená plocha uvnitř čtverce o straně 6 cm, pokud každá ze čtyř hnědých kruhových úsečí je z kruhu o poloměru délky stany čtverce? Délka kruhových úsečí je rovna délce strany čtverce. Situace je vyobrazena na obrázku vpravo. - Stěnová výška
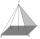 Aký je objem pravidelného čtyřbokého jehlanu, výška jehlanu 30 cm a stěnová výška je 50 cm?
Aký je objem pravidelného čtyřbokého jehlanu, výška jehlanu 30 cm a stěnová výška je 50 cm? - Trojúhelníku 63244
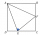 Obsah Čtverce ABCD na obrázku je 36 cm². Jaký je v cm² obsah trojúhelníku AEF, pokud body E a F jsou středy stran čtverce BC a CD?
Obsah Čtverce ABCD na obrázku je 36 cm². Jaký je v cm² obsah trojúhelníku AEF, pokud body E a F jsou středy stran čtverce BC a CD? - Jak dlouhá
 Jak dlouhá je úhlopříčka čtverce se stranou a=50mm?
Jak dlouhá je úhlopříčka čtverce se stranou a=50mm? - Je dán 13
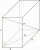 Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH.
Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH. - Čtvercovou 44061
 Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška.
Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška. - K MDŽ
 Srdce maminkám k MDŽ snadno vyrobíme tak, že ke dvěma horním stranám čtverce stojícím na svém vrcholu přikreslíme dva půlkruhy. Jaký poloměr bude mít kružnice opsaná tomuto srdci, když délka strany čtverce je rovna 1?
Srdce maminkám k MDŽ snadno vyrobíme tak, že ke dvěma horním stranám čtverce stojícím na svém vrcholu přikreslíme dva půlkruhy. Jaký poloměr bude mít kružnice opsaná tomuto srdci, když délka strany čtverce je rovna 1? - Jehlan
 Pravidelný 4-boky jehlan má tělesových výšku 2 dm a protilehlé boční hrany svírají úhel 70°. Vypočtěte povrch a objem jehlanu.
Pravidelný 4-boky jehlan má tělesových výšku 2 dm a protilehlé boční hrany svírají úhel 70°. Vypočtěte povrch a objem jehlanu. - Čtvercovým 42981
 Lze z kmene o průměru 42 cm vyříznout trám se čtvercovým průřezem o straně délky 30 cm? Odpověď zapiš způsobem: ano, neboť. .. . . ne, neboť. ..
Lze z kmene o průměru 42 cm vyříznout trám se čtvercovým průřezem o straně délky 30 cm? Odpověď zapiš způsobem: ano, neboť. .. . . ne, neboť. .. - Je dán 11
 Je dán čtverec ABCD a bod E ležící vně daného čtverce. Jaká je plocha čtverce když platí že vzdálenost |AE| = 2, |DE| = 5 a |BE| = 4.
Je dán čtverec ABCD a bod E ležící vně daného čtverce. Jaká je plocha čtverce když platí že vzdálenost |AE| = 2, |DE| = 5 a |BE| = 4. - Úhlopříčka 40091
 Vypočítej velikost hrany kostky, pokud úhlopříčka stěny je 8 cm.
Vypočítej velikost hrany kostky, pokud úhlopříčka stěny je 8 cm.
