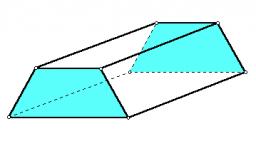
Vodní kanál
Průřez vodního kanálu je lichoběžník. Šířka dna je 19,7 m, šířka vodní hladiny je 28,5 m, boční stěny mají sklon 67°30' a 61°15'. Vypočtěte, jaké množství vody proteče kanálem za 5 minut, pokud rychlost vodního proudu je 0,3 m/s.
Správná odpověď:
Zobrazuji 1 komentář:
Tipy na související online kalkulačky
Základem výpočtů v analytické geometrii je dobrá kalkulačka rovnice přímky, která ze souřadnic dvou bodů v rovině vypočítá smernicový, normálový i parametrický tvar přímky, směrnici, směrový úhel, směrový vektor, délku úsečky, průsečíky se souřadnicovým osami atd.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Chcete proměnit jednotku rychlosti?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Chcete proměnit jednotku rychlosti?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- stereometrie
- hranol
- planimetrie
- pravoúhlý trojúhelník
- trojúhelník
- lichoběžník
- sinusová věta
- goniometrie a trigonometrie
- sinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Letadlo 13
 Letadlo letělo z letiště m pod kurzem 132° do letiště n, pak z n do p pod kurzem 235°. Vzdálenost letišť mn je 380 km, np 284 km. Jaký bude kurz návratu do m a jaká je vzdálenost letišť pm?
Letadlo letělo z letiště m pod kurzem 132° do letiště n, pak z n do p pod kurzem 235°. Vzdálenost letišť mn je 380 km, np 284 km. Jaký bude kurz návratu do m a jaká je vzdálenost letišť pm? - Pozorovatelně 71934
 Letadlo letící směrem k pozorovatelně, z ní bylo zaměřeno v přímé vzdálenosti 5300 m pod výškovým úhlem 28º a po 9 sekundách v přímé vzdálenosti 2400 m pod výškovým úhlem 50º. Vypočítejte vzdálenost, kterou v tomto časovém intervalu letadlo prolétlo, jeho
Letadlo letící směrem k pozorovatelně, z ní bylo zaměřeno v přímé vzdálenosti 5300 m pod výškovým úhlem 28º a po 9 sekundách v přímé vzdálenosti 2400 m pod výškovým úhlem 50º. Vypočítejte vzdálenost, kterou v tomto časovém intervalu letadlo prolétlo, jeho - Vzdálenost 71874
 Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla.
Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla. - Z věže
 Z věže 15m vysoké a od řeky 30 m se jevila šířka řeky v úhlu 15°. Jak široká je řeka v tomto místě?
Z věže 15m vysoké a od řeky 30 m se jevila šířka řeky v úhlu 15°. Jak široká je řeka v tomto místě? - Adam (A)
 Adam (A) stojí na jednom břehu řeky, Bedřich (B) stojí na druhém. Aby mohla být stanovena jejich vzdálenost, byla na jednom břehu řeky změřena základna AC o délce 136 m a úhly CAB s velikostí 70°21´ a ACB s velikostí 43°44´. Jaká je vzdálenost Adama a Bed
Adam (A) stojí na jednom břehu řeky, Bedřich (B) stojí na druhém. Aby mohla být stanovena jejich vzdálenost, byla na jednom břehu řeky změřena základna AC o délce 136 m a úhly CAB s velikostí 70°21´ a ACB s velikostí 43°44´. Jaká je vzdálenost Adama a Bed - Trojúhelníku 64704
 V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'.
V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'. - Kosinusova
 Kosinusova a sinusova věta: Vypočítejte všechny chybějící hodnoty v trojúhelníku ABC. c = 2,9 cm; β = 28°; γ = 14°α =? °; a =? cm; b =? cm
Kosinusova a sinusova věta: Vypočítejte všechny chybějící hodnoty v trojúhelníku ABC. c = 2,9 cm; β = 28°; γ = 14°α =? °; a =? cm; b =? cm - Kosinusova
 Kosinusova a sinusova věta : Vypočítejte všechny chybějící hodnoty z trojúhelníku ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Kosinusova a sinusova věta : Vypočítejte všechny chybějící hodnoty z trojúhelníku ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - V trojúhelníku
 V trojúhelníku ABC vypočítejte velikosti všech výšek, úhlů, obvod a obsah, pokud je dané a-40cm, b-57cm, c-59cm
V trojúhelníku ABC vypočítejte velikosti všech výšek, úhlů, obvod a obsah, pokud je dané a-40cm, b-57cm, c-59cm - Ťežišťe a obsah
 V trojúhelníku ABC jsou dány délky jeho těžnic tc = 9, ta = 6. Označme T průsečík těžnic, S střed strany BC. Velikost úhlu CTS je 60°. Vypočítejte délku strany BC s přesností na 2 desetinná místa.
V trojúhelníku ABC jsou dány délky jeho těžnic tc = 9, ta = 6. Označme T průsečík těžnic, S střed strany BC. Velikost úhlu CTS je 60°. Vypočítejte délku strany BC s přesností na 2 desetinná místa. - Letiště
 Z letiště odletí současně dvě letadla, první s kurzem 30° a druhé s kurzem 86°. Obě letí rychlostí 330 km/h. Kolik budou od sebe vzdáleny za 45 minut letu?
Z letiště odletí současně dvě letadla, první s kurzem 30° a druhé s kurzem 86°. Obě letí rychlostí 330 km/h. Kolik budou od sebe vzdáleny za 45 minut letu? - 3úhelník 35881
 Součet délek dvou stran b+c=12 cm Úhel beta=68 Úhel gama=42 narysuj 3úhelník ABC
Součet délek dvou stran b+c=12 cm Úhel beta=68 Úhel gama=42 narysuj 3úhelník ABC - Zorný úhel
 Pozorovatel vidí přímou ohradu dlouhou 60 m v zorném úhlu 30°. Od jednoho konce ohrady je vzdálen 102 m. Jak daleko je pozorovatel od druhého konce ohrady?
Pozorovatel vidí přímou ohradu dlouhou 60 m v zorném úhlu 30°. Od jednoho konce ohrady je vzdálen 102 m. Jak daleko je pozorovatel od druhého konce ohrady? - Trojúhelníku 18223
 Ze sinusové věty urč poměr velikostí stran trojúhelníku, jehož úhly jsou 30°, 60°, 90°.
Ze sinusové věty urč poměr velikostí stran trojúhelníku, jehož úhly jsou 30°, 60°, 90°. - Poměr stran
 Poměr stran pravoúhlého trojúhelníku je 13: 12: 5. Vypočítejte vnitřní úhly trojúhelníku.
Poměr stran pravoúhlého trojúhelníku je 13: 12: 5. Vypočítejte vnitřní úhly trojúhelníku. - Trojúhelníku 9731
 Řešte trojúhelník ABC, pokud strana a = 52 cm, výška na druhou stranu je vb = 21 cm a obsah trojúhelníku je S = 330 cm² .
Řešte trojúhelník ABC, pokud strana a = 52 cm, výška na druhou stranu je vb = 21 cm a obsah trojúhelníku je S = 330 cm² . - Pozorovatel 8202
 Pozorovatel sleduje z vrcholu kopce, který je 75 m nad hladinou jezera, dvě loďky v hloubkových úhlech 64° a 48°. Určete vzdálenost mezi loďkami, pokud obě loďky a pozorovatel jsou ve stejné svislé rovině.
Pozorovatel sleduje z vrcholu kopce, který je 75 m nad hladinou jezera, dvě loďky v hloubkových úhlech 64° a 48°. Určete vzdálenost mezi loďkami, pokud obě loďky a pozorovatel jsou ve stejné svislé rovině.
