MO Z6-I-2 2017
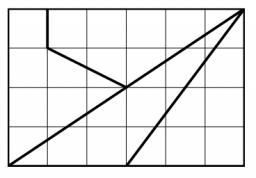
Erika chtěla nabídnout čokoládu svým třem kamarádkám. Když ji vytáhla z batohu, zjistila, že je polámaná jako na obrázku. (Vyznačené čtverečky jsou navzájem shodné.) Dívky se dohodly, že čokoládu dále lámat nebudou a losem určí, jak velký kousek která dostane. Seřaďte čtyři kousky čokolády od nejmenšího po největší
Správná odpověď:
Zobrazuji 3 komentáře:
Dr Math
S1 = je obsah trojúhelníku vpravo dole, základna 3, vyska 4 ....
S2 = je obsah trojúhelníku vlevo dole, opět základna 3 a výška 4 ...
S3 je obsah 4-úhelníka vpravo nahoře co vypadá téměř jako trojúhelník. Sklada se z odcitani obsahů dvou trojúhelníků.
a) trojúhelník o zakladne 7 a vyske 2. Zakladna 7 (obdélníku má delší stranu jen 6) proto, protože prodloužení čáry směřující vlevo nahoře protne prodloužené stranu obdélníku, tak že zformuje trojúhelník o zakladni 7 .... tj. o jeden dílek vlevo od horního levého vrcholu obdélníku. Jinými slovy cara směřujícím vlevo nahoře, jedoucím ve sklonu 1 dílek vertikalni ke 2 horizontálně protne prodloužené stranu obdélníka az 1 dílek od vrcholu.
b) a musíme odečíst obsah pravoúhleho trojúhelníka o odvěsně 1 a druhé odvěsně 2.
S4 je obsah obdélník minus S1 + S2 + S3 (Zbývajících plocha)
S2 = je obsah trojúhelníku vlevo dole, opět základna 3 a výška 4 ...
S3 je obsah 4-úhelníka vpravo nahoře co vypadá téměř jako trojúhelník. Sklada se z odcitani obsahů dvou trojúhelníků.
a) trojúhelník o zakladne 7 a vyske 2. Zakladna 7 (obdélníku má delší stranu jen 6) proto, protože prodloužení čáry směřující vlevo nahoře protne prodloužené stranu obdélníku, tak že zformuje trojúhelník o zakladni 7 .... tj. o jeden dílek vlevo od horního levého vrcholu obdélníku. Jinými slovy cara směřujícím vlevo nahoře, jedoucím ve sklonu 1 dílek vertikalni ke 2 horizontálně protne prodloužené stranu obdélníka az 1 dílek od vrcholu.
b) a musíme odečíst obsah pravoúhleho trojúhelníka o odvěsně 1 a druhé odvěsně 2.
S4 je obsah obdélník minus S1 + S2 + S3 (Zbývajících plocha)
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Vzdálenost 71874
 Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla.
Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla. - Půda - tyče
 Nedávno jsem uklízel půdu a našel jsem sadu nejméně 14 tyčinek, které mi před několika lety prodal jeden zvědavý Ital. Když jsem se usilovně snažil přijít na to, proč jsem to od něj koupil, uvědomil jsem si, že sada má tu neuvěřitelnou vlastnost, že neexi
Nedávno jsem uklízel půdu a našel jsem sadu nejméně 14 tyčinek, které mi před několika lety prodal jeden zvědavý Ital. Když jsem se usilovně snažil přijít na to, proč jsem to od něj koupil, uvědomil jsem si, že sada má tu neuvěřitelnou vlastnost, že neexi - Po vodorovné
 Po vodorovné trati jede auto stálou rychlostí 20 m∙s–1. Prší. Kapky deště padají ve svislém směru rychlostí o velikosti 6 m∙s–1. a) Jak velká je rychlost kapek vzhledem k oknům auta? b) Jaký úhel svírají stopy dešťových kapek na okně auta se svislým směre
Po vodorovné trati jede auto stálou rychlostí 20 m∙s–1. Prší. Kapky deště padají ve svislém směru rychlostí o velikosti 6 m∙s–1. a) Jak velká je rychlost kapek vzhledem k oknům auta? b) Jaký úhel svírají stopy dešťových kapek na okně auta se svislým směre - Na kružnici
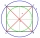 Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC.
Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC. - Rovnoramenného 48443
 Tři stejné kladné náboje Q jsou umístěny ve vrcholech rovnoramenného pravoúhlého trojúhelníku ABC. Pravý úhel je u vrcholu A. Délka strany AB je 1m. Jaká je intenzita elektrického pole ve středu S strany BC, t. J. jaká síla by působila na kladný náboj q v
Tři stejné kladné náboje Q jsou umístěny ve vrcholech rovnoramenného pravoúhlého trojúhelníku ABC. Pravý úhel je u vrcholu A. Délka strany AB je 1m. Jaká je intenzita elektrického pole ve středu S strany BC, t. J. jaká síla by působila na kladný náboj q v - Výslednice 3
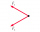 Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°.
Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°. - Z8–I–5 MO 2019
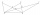 Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c
Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c - Součet obsahů
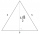 Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr
Nád výškou rovnostranného trojúhelníku ABC je sestrojen rovnostranný trojúhelník A1, B1, C1, nad jeho výškou je sestrojen rovnostranný trojúhelník A2, B2, C2, atd. Se postup neustále opakuje. Jaký je velký součet obsahů všech trojúhelníků, pokud strana tr - Motorový člun
 Motorový člun se pohybuje vzhledem k vodě stálou rychlostí 13 m/s. Rychlost vodního proudu v řece je 5 m/s a) Pod jakým úhlem vzhledem k vodnímu proudu musí člun plout, aby se stále pohyboval kolmo ke břehům řeky? b) Jak velkou rychlostí se přibližuje člu
Motorový člun se pohybuje vzhledem k vodě stálou rychlostí 13 m/s. Rychlost vodního proudu v řece je 5 m/s a) Pod jakým úhlem vzhledem k vodnímu proudu musí člun plout, aby se stále pohyboval kolmo ke břehům řeky? b) Jak velkou rychlostí se přibližuje člu - Lodník
 Po palubě lodí kráčí lodník stálou rychlostí 5 km/h ve směru, který svírá se směrem rychlosti lodi úhel 60°. Loď se pohybuje vzhledem ke klidné hladině jezera stálou rychlostí 10 km/h. Určete graficky velikost rychlosti, kterou se lodník pohybuje vzhledem
Po palubě lodí kráčí lodník stálou rychlostí 5 km/h ve směru, který svírá se směrem rychlosti lodi úhel 60°. Loď se pohybuje vzhledem ke klidné hladině jezera stálou rychlostí 10 km/h. Určete graficky velikost rychlosti, kterou se lodník pohybuje vzhledem - Sčítaní rychlostí
 V železničním voze rychlíku jedoucího stálou rychlostí 24 m/s vrhneme míček, jehož počáteční rychlost vzhledem k vozu je 7 m/s. Jak velká je počáteční rychlost míčku vzhledem k povrchu země, jestliže ho vrhneme a) ve směru jízdy b) proti směru jízdy c) ko
V železničním voze rychlíku jedoucího stálou rychlostí 24 m/s vrhneme míček, jehož počáteční rychlost vzhledem k vozu je 7 m/s. Jak velká je počáteční rychlost míčku vzhledem k povrchu země, jestliže ho vrhneme a) ve směru jízdy b) proti směru jízdy c) ko - Parašutista
 Po otevření padáku klesá výsadkář k zemi stálou rychlostí 2 m/s, přičemž ho unáší boční vítr stálou rychlostí 1,5 m/s. Určete: a) velikost jeho výsledné rychlosti vzhledem k zemi, b) vzdálenost místa jeho dopadu od osamělého stromu, nad nímž se nacházel v
Po otevření padáku klesá výsadkář k zemi stálou rychlostí 2 m/s, přičemž ho unáší boční vítr stálou rychlostí 1,5 m/s. Určete: a) velikost jeho výsledné rychlosti vzhledem k zemi, b) vzdálenost místa jeho dopadu od osamělého stromu, nad nímž se nacházel v - Mnohoúhelník - hexagon
 V šestistranném polygonu - mnohoúhelníku platí - první dva úhly jsou stejné, třetí úhel je dvojnásobný (stejných úhlů), dva další úhly jsou trojnásobkem stejného úhlu, zatímco poslední úhel je pravý úhel. Najděte hodnotu každého úhlu.
V šestistranném polygonu - mnohoúhelníku platí - první dva úhly jsou stejné, třetí úhel je dvojnásobný (stejných úhlů), dva další úhly jsou trojnásobkem stejného úhlu, zatímco poslední úhel je pravý úhel. Najděte hodnotu každého úhlu. - Vzdálenosti 4529
 Chlapec vesluje na loďce rychlostí velikosti 7,2 km/h. Loďku nasměroval kolmo na protilehlý břeh vzdálený 600m. Řeka unáší loďku rychlostí 4,0 km/h. Jaká je výsledná rychlost loďky vzhledem ke břehu? Jak daleko unese řeka loďku od místa, kde by měla loďka
Chlapec vesluje na loďce rychlostí velikosti 7,2 km/h. Loďku nasměroval kolmo na protilehlý břeh vzdálený 600m. Řeka unáší loďku rychlostí 4,0 km/h. Jaká je výsledná rychlost loďky vzhledem ke břehu? Jak daleko unese řeka loďku od místa, kde by měla loďka - Útvar
 Vypočítejte obsah rovinného geometrického útvaru, jehož libovolný bod je od úsečky AB vzdálen nejvýše 3 cm. Délka úsečky AB je 5 cm.
Vypočítejte obsah rovinného geometrického útvaru, jehož libovolný bod je od úsečky AB vzdálen nejvýše 3 cm. Délka úsečky AB je 5 cm. - Výslednice sil
 Vypočtěte matematicky a graficky výslednici soustavy tří sil se společným působištěm, jestliže: F1 = 50kN α1 = 30° F2 = 40kN α2 = 45° F3 = 40kN α3 = 25°
Vypočtěte matematicky a graficky výslednici soustavy tří sil se společným působištěm, jestliže: F1 = 50kN α1 = 30° F2 = 40kN α2 = 45° F3 = 40kN α3 = 25°
