Javy
Jev C je jev s pravděpodobností 0,79. Jaká je pravděpodobnost, že jev C poprvé nastane při 7, 9, 3 pokuse.
Správná odpověď:

Zobrazuji 4 komentáře:
Ichad
Špatné zadání. Je to myšleno ve smyslu: "Jaká je pst, že jev I nastane !!poprvé!! při N-tém pokusu."
Tak jak je to zadané je odpověď 36 % (při každém nezávislém pokusu je stejná).
Zde je ale řešením řetězec (N-1)-krát nenastane a poté nastane..
Tak jak je to zadané je odpověď 36 % (při každém nezávislém pokusu je stejná).
Zde je ale řešením řetězec (N-1)-krát nenastane a poté nastane..
Tipy na související online kalkulačky
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Chceš si dát spočítat kombinační číslo?
Chceš si dát spočítat kombinační číslo?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Určete 51
 Určete, jaká bude nutná tloušťka stínícího materiálu, máme-li snížit záření na 3% původní hodnoty, jestliže víme, že tloušťka materiálu 6 mm sníží úroveň téhož záření o 9%. Zaokrouhlete na celou hodnotu v milimetrech směrem nahoru (na vyšší hodnotu).
Určete, jaká bude nutná tloušťka stínícího materiálu, máme-li snížit záření na 3% původní hodnoty, jestliže víme, že tloušťka materiálu 6 mm sníží úroveň téhož záření o 9%. Zaokrouhlete na celou hodnotu v milimetrech směrem nahoru (na vyšší hodnotu). - Počet 5
 Počet obyvatel města klesl za 10 let z 72800 na 56000. Jaký je roční úbytek obyvatel v procentech?
Počet obyvatel města klesl za 10 let z 72800 na 56000. Jaký je roční úbytek obyvatel v procentech? - Radioaktivního 74344
 Typ radioaktivního prvku má hmotnost 1,125 gramu. Při analýze se zjistí, že je mu 405 let. Pokud se tento radioaktivní prvek každých 45 let rozpadne o polovinu, zjistěte, kolik gramů tohoto radioaktivního prvku bylo před 405 lety.
Typ radioaktivního prvku má hmotnost 1,125 gramu. Při analýze se zjistí, že je mu 405 let. Pokud se tento radioaktivní prvek každých 45 let rozpadne o polovinu, zjistěte, kolik gramů tohoto radioaktivního prvku bylo před 405 lety. - Sedmisegmentovku 73834
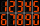 Elektronické zařízení někdy používají níže uvedený typ číslic - sedmisegmentovku, kde každá číslice používá několik krátkých svítících proužků, například sedm používá tři malé proužky. Jaké je největší trojciferné číslo, které můžete vytvořit, použijete-l
Elektronické zařízení někdy používají níže uvedený typ číslic - sedmisegmentovku, kde každá číslice používá několik krátkých svítících proužků, například sedm používá tři malé proužky. Jaké je největší trojciferné číslo, které můžete vytvořit, použijete-l
- V=4x^3+43x^2+63x 72764
 Největší vnitřní akvárium na světě. Ve své obrovské nádrži s kapacitou reprezentovanou následujícím polynomem V=4x³+43x²+63x Akvárium má tvar obdélníkového hranolu. Najděte následující: 1. Je-li výška akvária x, najděte plochu základny (B). 2. Na základě
Největší vnitřní akvárium na světě. Ve své obrovské nádrži s kapacitou reprezentovanou následujícím polynomem V=4x³+43x²+63x Akvárium má tvar obdélníkového hranolu. Najděte následující: 1. Je-li výška akvária x, najděte plochu základny (B). 2. Na základě - Konečná posloupnost
 Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: a1=18, an=13122, sn=19674, n=?, q=?
Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: a1=18, an=13122, sn=19674, n=?, q=? - Poseidon
 Poseidon vložil 2 747 zlatých drachem na spořicí účet univerzity Mount Olympus, aby zajistil, že Percy může jít na vysokou školu. Platí roční úroky 0,04 (v desetinné podobě). Po 11 letech vybere peníze. O kolik více peněz by měl, kdyby se úrok vyplácel sp
Poseidon vložil 2 747 zlatých drachem na spořicí účet univerzity Mount Olympus, aby zajistil, že Percy může jít na vysokou školu. Platí roční úroky 0,04 (v desetinné podobě). Po 11 letech vybere peníze. O kolik více peněz by měl, kdyby se úrok vyplácel sp - Počet
 Počet obyvatel města je 56 000. Každý rok klesá o 2%. Jaký bude počet obyvatel města po 13 letech?
Počet obyvatel města je 56 000. Každý rok klesá o 2%. Jaký bude počet obyvatel města po 13 letech? - Roční přírůstek
 Počet vyrobených aut vzrostl za 3 roky z 45 000 na 47 000. Vypočítejte, jaký byl průměrný roční přírůstek aut v%.
Počet vyrobených aut vzrostl za 3 roky z 45 000 na 47 000. Vypočítejte, jaký byl průměrný roční přírůstek aut v%.
- Na stránkách
 Na stránkách ČSÚ se můžeme dozvědět, že v roce 1869 měla Praha i s předměstími celkem 10 947 domů a v roce 1900 už 18 838 domů. Jaký byl každoroční procentuální „přírůstek“ domů v Praze mezi lety 1869 až 1900, jestliže uvažujeme konstantní procentuální „p
Na stránkách ČSÚ se můžeme dozvědět, že v roce 1869 měla Praha i s předměstími celkem 10 947 domů a v roce 1900 už 18 838 domů. Jaký byl každoroční procentuální „přírůstek“ domů v Praze mezi lety 1869 až 1900, jestliže uvažujeme konstantní procentuální „p - Členy GP
 Jaký je 5. člen geometrické posloupnosti, pokud je 8. člen 80 a společný poměr (kvocient) r = 1/2?
Jaký je 5. člen geometrické posloupnosti, pokud je 8. člen 80 a společný poměr (kvocient) r = 1/2? - Procentuální přírůstek
 Jaký je roční procentuální přírůstek ve městě kdy se za 20 let zvýšil počet obyvatel na trojnásobek?
Jaký je roční procentuální přírůstek ve městě kdy se za 20 let zvýšil počet obyvatel na trojnásobek? - Tři ženy
 Uvádí se, že 72% pracujících žen používá počítače v práci. Vyberte si 3 ženy náhodně, zjistěte pravděpodobnost, že všechny 3 ženy budou při práci používat počítač.
Uvádí se, že 72% pracujících žen používá počítače v práci. Vyberte si 3 ženy náhodně, zjistěte pravděpodobnost, že všechny 3 ženy budou při práci používat počítač. - Podnikatel
 Podnikatel Žahourek vložil do banky na účet s 4,5% ročním úrokem částku 450 000. Vypočítej jaká částka bude na účtu po třech letech.
Podnikatel Žahourek vložil do banky na účet s 4,5% ročním úrokem částku 450 000. Vypočítej jaká částka bude na účtu po třech letech.
- Střádaní
 Vkladatel chce pravidelně na začátku roku vložit do peněžního ústavu stejnou částku peněz a na konci desátého roku chce mít naspořených 10 000 eur. Jakou částku má vkládat, pokud roční úroková míra ročního úrokovacieho období je 2% a daň z úroku je 19%? P
Vkladatel chce pravidelně na začátku roku vložit do peněžního ústavu stejnou částku peněz a na konci desátého roku chce mít naspořených 10 000 eur. Jakou částku má vkládat, pokud roční úroková míra ročního úrokovacieho období je 2% a daň z úroku je 19%? P - V geometrické binární
 V geometrické posloupnosti je dáno : kvocient q = 1/2 a součet prvních šest členů S6=63. Určete pátý prvek a5.
V geometrické posloupnosti je dáno : kvocient q = 1/2 a součet prvních šest členů S6=63. Určete pátý prvek a5. - Přírůstek dřeva
 Každým rokem se ve stejnou dobu zjišťuje přírůstek objemu dřeva v lese. Přírůstek činí pravidelně p% proti předchozímu roku. Jestliže se za 10 let zvětšil objem dřeva o 10%, jaké je číslo p?
Každým rokem se ve stejnou dobu zjišťuje přírůstek objemu dřeva v lese. Přírůstek činí pravidelně p% proti předchozímu roku. Jestliže se za 10 let zvětšil objem dřeva o 10%, jaké je číslo p?
