Divadlo
V divadle je v každé řadě vždy 20 sedadel. Vstupenka do prvních 3 řad stojí 180 KČ. Do dalších řad jsou vstupenky po 114 KČ. Představení bylo plně vyprodáno. Tržba činila 19920 KČ.
Kolik řad je v divadle?
Kolik řad je v divadle?
Správná odpověď:

Zobrazuji 3 komentáře:
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Vzdálenost 145
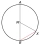 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Rovnice 47
 Rovnice se zlomkama: 3y - y+3/4 = 1+y/2
Rovnice se zlomkama: 3y - y+3/4 = 1+y/2 - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Vypočítej 83251
 Vypočítej obvod čtverce, jehož obsah je 25 dm² .
Vypočítej obvod čtverce, jehož obsah je 25 dm² .
- Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku. - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm. - Obdélníku 83176
 Pokud zmenšíme délku obdélníku o 2cm a šířku o 1cm, tak se obsah obdélníku zmenší o 8 cm². Pokud zvětšíme délku obdélníku o 1cm a šířku o 2cm, tak se obsah obdélníku zvětší o 13 cm². Jaké byly původní rozměry obdélníku?
Pokud zmenšíme délku obdélníku o 2cm a šířku o 1cm, tak se obsah obdélníku zmenší o 8 cm². Pokud zvětšíme délku obdélníku o 1cm a šířku o 2cm, tak se obsah obdélníku zvětší o 13 cm². Jaké byly původní rozměry obdélníku?
- Obrazec
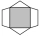 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Zatáčka 3
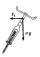 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Katka 7
 Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá
Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá - Kladivo 2
 Kladivo o hmotnosti 600g dopadlo na hlavičku hřebíku rychlostí 5 m/s. Jak velká je průměrná odporová síla zdiva, jestliže hřebík vnikl 3 cm do zdi?
Kladivo o hmotnosti 600g dopadlo na hlavičku hřebíku rychlostí 5 m/s. Jak velká je průměrná odporová síla zdiva, jestliže hřebík vnikl 3 cm do zdi?
- Beranidlo
 Beranidlo s hmotností 400g padá z výšky 3 m. Při nárazu zarazí kůl do hloubky 60 cm. Jak velká je průměrná síla přemáhající odpor půdy?
Beranidlo s hmotností 400g padá z výšky 3 m. Při nárazu zarazí kůl do hloubky 60 cm. Jak velká je průměrná síla přemáhající odpor půdy? - Sud, kbelík, konvička
 Vnitřní objem sudu je 15krát větší než objem kbelíku. Objem kbelíku je 5krát větší než objem konvičky. Ze sudu plného vody jsme třetinu vody odebrali, takže v něm zbylo 60 litrů vody. Vypočtěte v litrech objem konvičky.
Vnitřní objem sudu je 15krát větší než objem kbelíku. Objem kbelíku je 5krát větší než objem konvičky. Ze sudu plného vody jsme třetinu vody odebrali, takže v něm zbylo 60 litrů vody. Vypočtěte v litrech objem konvičky. - Morská vs sladká
 Nákladní člun o celkové hmotnosti 4500t připlul z řeky do moře. Vypočtěte, o kolik tun je možno zvětšit hmotnost nákladu na člunu na moři, aby ponor zůstal stejný jako v řece. Hustota říční vody je 998 kg/m³. Hustota mořské vody je 1031 kg/m³. Príklad na
Nákladní člun o celkové hmotnosti 4500t připlul z řeky do moře. Vypočtěte, o kolik tun je možno zvětšit hmotnost nákladu na člunu na moři, aby ponor zůstal stejný jako v řece. Hustota říční vody je 998 kg/m³. Hustota mořské vody je 1031 kg/m³. Príklad na
