Na trasu
Na trasu dlouhou 182 km vyjelo v 9 hodin auto A, v 9:30 auto B a 9:45 auto C. Do cíle dojela všechna tři auta najednou. Průměrné rychlosti aut A a B se lišily o 6,5 km/h. O kolik se lišily průměrné rychlosti aut A a C?
Správná odpověď:

Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Chcete proměnit jednotku délky?
Chcete proměnit jednotku rychlosti?
Chcete proměnit jednotky času, např. hodiny na minuty?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Chcete proměnit jednotku délky?
Chcete proměnit jednotku rychlosti?
Chcete proměnit jednotky času, např. hodiny na minuty?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Poměr 51
 Poměr vzdálenosti nejbližšího a nejvzdálenějšího bodu kružnice, která je popsána rovnicí x2+y2-16x-12y+75=0 od počátku soustavy souřadnic je?
Poměr vzdálenosti nejbližšího a nejvzdálenějšího bodu kružnice, která je popsána rovnicí x2+y2-16x-12y+75=0 od počátku soustavy souřadnic je? - Čtvercovou 63174
 Urči součet délek všech hran kvádru se čtvercovou podstavou o obsahu 36 dm2, pokud jeho výška je 1/3 délky hrany jeho podstavy.
Urči součet délek všech hran kvádru se čtvercovou podstavou o obsahu 36 dm2, pokud jeho výška je 1/3 délky hrany jeho podstavy. - Raketa
 Vystřelí se raketa rychlostí 100 fps ve směru 30° nad vodorovnou rovinu. Určete maximální výšku, do které stoupá? Fps je jednotka stopa za sekundu.
Vystřelí se raketa rychlostí 100 fps ve směru 30° nad vodorovnou rovinu. Určete maximální výšku, do které stoupá? Fps je jednotka stopa za sekundu. - Na schodišti
 Na schodišti vysokém 3,6 metrů by se počet schodů zvětšil o 3, kdyby se výška jednoho schodu zmenšila o 4 cm. Jak jsou schody vysoké?
Na schodišti vysokém 3,6 metrů by se počet schodů zvětšil o 3, kdyby se výška jednoho schodu zmenšila o 4 cm. Jak jsou schody vysoké? - V rovnoramenném trojúhelníku
 V rovnoramenném trojúhelníku ABC se základnou AB; A [-3,4]; B [1,6] leží vrchol C na přímce 5x - 6y - 16 = 0. Vypočítejte souřadnice vrcholu C.
V rovnoramenném trojúhelníku ABC se základnou AB; A [-3,4]; B [1,6] leží vrchol C na přímce 5x - 6y - 16 = 0. Vypočítejte souřadnice vrcholu C. - Rozhledna
 Jak vysoká je rozhledna? Kdyby byl každý schod o 3 cm nižší, bylo by je na rozhlednu o 60 více. Kdyby byl zase o 3 cm vyšší, bylo by je o 40 méně, než jich je nyní.
Jak vysoká je rozhledna? Kdyby byl každý schod o 3 cm nižší, bylo by je na rozhlednu o 60 více. Kdyby byl zase o 3 cm vyšší, bylo by je o 40 méně, než jich je nyní. - Čtverec ABCD
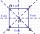 Je dán čtverec ABCD s délkou strany 100 mm. Vypočítej poloměr kružnice, která prochází vrcholy B, C a středem strany AD.
Je dán čtverec ABCD s délkou strany 100 mm. Vypočítej poloměr kružnice, která prochází vrcholy B, C a středem strany AD. - Na mapě 6
 Na mapě s měřítkem 1 : 5 000 je zobrazeno obdélníkové pole o výměře 18 ha. Délka pole je trojnásobkem jeho šířky. Plocha pole na mapě je 72 cm čtverečních. Jaká je skutečná délka a šířka pole?
Na mapě s měřítkem 1 : 5 000 je zobrazeno obdélníkové pole o výměře 18 ha. Délka pole je trojnásobkem jeho šířky. Plocha pole na mapě je 72 cm čtverečních. Jaká je skutečná délka a šířka pole? - V pravoúhlém 4
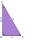 V pravoúhlém trojúhelníku je délka přepony 65 m a rozdíl odvěsen 23 m. Vypočítejte obvod tohoto trojúhelníku.
V pravoúhlém trojúhelníku je délka přepony 65 m a rozdíl odvěsen 23 m. Vypočítejte obvod tohoto trojúhelníku. - Délka úseku úsečky
 Předpokládejme, že víte, že délka úseku úsečky je 15, x2 = 6, y2 = 14 a x1 = -3. Najděte možnou hodnotu y1. Existuje více než jedna možná odpověď? Proč ano nebo proč ne?
Předpokládejme, že víte, že délka úseku úsečky je 15, x2 = 6, y2 = 14 a x1 = -3. Najděte možnou hodnotu y1. Existuje více než jedna možná odpověď? Proč ano nebo proč ne? - Pole obdélník
 Pole ve tvaru obdélníka má délku 119 m a šířku 19 m. O kolik se musí zkrátit jeho délka a zvětšit jeho šířka, aby jeho plocha zůstala zachována a jeho obvod se zvětšil o 24 m?
Pole ve tvaru obdélníka má délku 119 m a šířku 19 m. O kolik se musí zkrátit jeho délka a zvětšit jeho šířka, aby jeho plocha zůstala zachována a jeho obvod se zvětšil o 24 m? - Výška trojúhelníku
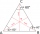 Vrcholy rovnostranného trojúhelníku leží na 3 různých rovnoběžkách. Prostřední je od krajních vzdálena 5 m, resp. 3 m. Vypočítejte výšku tohoto trojúhelníku.
Vrcholy rovnostranného trojúhelníku leží na 3 různých rovnoběžkách. Prostřední je od krajních vzdálena 5 m, resp. 3 m. Vypočítejte výšku tohoto trojúhelníku. - Dve tětivy
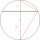 Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm.
Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm. - Zmenší-li
 Zmenší-li se délka stany čtvercové podložky o 6 cm, zmenší se její obsah o 2,76 dm². Urči délku strany původní i zmenšené podložky.
Zmenší-li se délka stany čtvercové podložky o 6 cm, zmenší se její obsah o 2,76 dm². Urči délku strany původní i zmenšené podložky. - V daném
 V daném obdélníku je délka o 12 m větší než šířka. Zmenšíme-li délku o 10 m a šířku zvětšíme o 2 m dostaneme čtverec. Plošný obsah původního obdélníku je o 300 m² větší než plošný obsah čtverce. Určete rozměry obdélníku.
V daném obdélníku je délka o 12 m větší než šířka. Zmenšíme-li délku o 10 m a šířku zvětšíme o 2 m dostaneme čtverec. Plošný obsah původního obdélníku je o 300 m² větší než plošný obsah čtverce. Určete rozměry obdélníku. - Nejlevnější 7976
 V rekreační oblasti se má postavit bazén ve tvaru kvádru o objemu 200m³. Jeho délka má být 4-násobkem šířky, přičemž cena 1 m² dna bazénu je 2-krát levnější než 1 m² stěny bazénu. Jaké rozměry musí mít bazén, aby stavba byla nejlevnější?
V rekreační oblasti se má postavit bazén ve tvaru kvádru o objemu 200m³. Jeho délka má být 4-násobkem šířky, přičemž cena 1 m² dna bazénu je 2-krát levnější než 1 m² stěny bazénu. Jaké rozměry musí mít bazén, aby stavba byla nejlevnější? - Dva cyklisté
 Současně dva cyklisté opustili města A a B při konstantních rychlostech. První z města A do města B a druhý z města B do města A. Na jednom místě cesty se setkali. Po setkání první cyklista přišel do města B za 36 minut, druhý cyklista přišel do města A z
Současně dva cyklisté opustili města A a B při konstantních rychlostech. První z města A do města B a druhý z města B do města A. Na jednom místě cesty se setkali. Po setkání první cyklista přišel do města B za 36 minut, druhý cyklista přišel do města A z
