Kružnice a tečna
Najděte rovnici kružnice se středem v (1,20), která se dotýká přímky 8x + 5y-19 = 0
Správná odpověď:
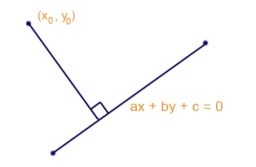
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Určete 20
 Určete velikost úhlu mezi vektory u =(3; -5) a v = (10;6)
Určete velikost úhlu mezi vektory u =(3; -5) a v = (10;6) - Je dán 15
 Je dán koncový bod vektoru, který je umístěn v počátku kartézské soustavy Oxy. Určete souřadnice vektoru, jeho velikost a načrtněte jej: P[3,4] ; Q[-2,7] ; S[-5,-2] . .. tj. Vektory PO, QO, SO
Je dán koncový bod vektoru, který je umístěn v počátku kartézské soustavy Oxy. Určete souřadnice vektoru, jeho velikost a načrtněte jej: P[3,4] ; Q[-2,7] ; S[-5,-2] . .. tj. Vektory PO, QO, SO - Určete 19
 Určete neznámou souřadnici vektoru tak, aby vektory byly kolineární: e=(7, -2), f = (-2, f2) c= ( -3/7, c2), d=(-4,0)
Určete neznámou souřadnici vektoru tak, aby vektory byly kolineární: e=(7, -2), f = (-2, f2) c= ( -3/7, c2), d=(-4,0) - Orientovanými 55871
 Složte dvě posunutí d1 a d2 znázorněná orientovanými úsečky OA a OB. Souřadnice bodů jsou O=(0m,0m), A=(3m,3m), B=(5m,2m). Změřte velikost výsledného posunutí d.
Složte dvě posunutí d1 a d2 znázorněná orientovanými úsečky OA a OB. Souřadnice bodů jsou O=(0m,0m), A=(3m,3m), B=(5m,2m). Změřte velikost výsledného posunutí d.
- Vektory v prostoru
 Dáno jsou vektory u = (1; 3; -4), v = (0; 1; 1). Určete velikost těchto vektorů, Vypočtěte úhel vektorů, vzdálenost mezi vektory.
Dáno jsou vektory u = (1; 3; -4), v = (0; 1; 1). Určete velikost těchto vektorů, Vypočtěte úhel vektorů, vzdálenost mezi vektory. - Abs a vektory
 Jsou dány vektory a=(4,2), b=(-2,1). Vypočítejte: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|.
Jsou dány vektory a=(4,2), b=(-2,1). Vypočítejte: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|. - Vzdálenost
 Vypočítejte vzdálenost bodu A [0, 2] od přímky procházející body B [9, 5] a C [1, -1].
Vypočítejte vzdálenost bodu A [0, 2] od přímky procházející body B [9, 5] a C [1, -1]. - Úhel tělesových úhlopříček
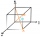 Pomocí vektorového skalárního součinu (tečky) produktu vypočítejte úhel tělesových úhlopříček kostky.
Pomocí vektorového skalárního součinu (tečky) produktu vypočítejte úhel tělesových úhlopříček kostky. - Vypočítejte: 8175
 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t
- Vypočítejte: 8174
 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době - Vypočítejte: 8173
 Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t2; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného b
Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t2; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného b - Vypočítejte: 8172
 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2s
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2s - Čtverec 28
 Čtverec ABCD má střed S[−3, −2] a vrchol A[1, −3]. Určete souřadnice ostatních vrcholů čtverce.
Čtverec ABCD má střed S[−3, −2] a vrchol A[1, −3]. Určete souřadnice ostatních vrcholů čtverce. - Vypočítejte 5
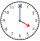 Vypočítejte velikost úhlu, které svírají přímky p a q, které spojují na ciferníku hodin 1, 6(přímka p) a 5, 8(přímka q)
Vypočítejte velikost úhlu, které svírají přímky p a q, které spojují na ciferníku hodin 1, 6(přímka p) a 5, 8(přímka q)
