Z9 – I – 2 MO 2018
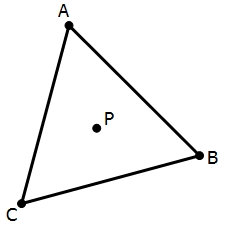
V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM.
Správná odpověď:
Zobrazuji 13 komentářů:
Žák
Nemá to být obecně, nebo těch 0,278 je, že zabírá tuto část?
Jakože kdyby byla odpoved 0,5 tak by to znamenalo že zabíra polovinu?
Jakože kdyby byla odpoved 0,5 tak by to znamenalo že zabíra polovinu?
Dr Math
jasne ze se to da obecne... jenomze s cislami se lepe pracuje... Da se dokazat ze tenhle priklad je invariantni ke delce "a", a proto jsme si zvolili a=1 a zjenodusili jsi zivot.... ve vyraze x=S4/S by se a2 vykratilo s a2 ... Je to aj nejaky princip analogie...
Dr Math
Je jedno ci odpoved napisem 5/18 nebo 27,8%.... Ta tretina patrne vyplyva ze "bod L leží v třetině strany" tak je tam nejaka podobnost...
Pepa
Je možnost že to můžeme vyřešit jako: troj. AKM 1/3*1/2=1/6
udělat to u všech a sečíst
udělat to u všech a sečíst
5 let 1 Like
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Z6–I–5 MO 2024
 Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru
Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - MO z5 2024
 Anetčin strýc má narozeniny ve stejný den v roce jako Anetčina teta. Strýc je starší než teta, ne však o víc než o deset let, a oba jsou plnoletí. Na poslední oslavě jejich narozenin si Anetka uvědomila, že když vynásobí jejich oslavované věky a výsledný
Anetčin strýc má narozeniny ve stejný den v roce jako Anetčina teta. Strýc je starší než teta, ne však o víc než o deset let, a oba jsou plnoletí. Na poslední oslavě jejich narozenin si Anetka uvědomila, že když vynásobí jejich oslavované věky a výsledný - Čtyřúhulník AFHD
 Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD.
Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD.
- Nepozornosti MO 2023 Z9
 Karel měl vynásobit dvě dvouciferná čísla. Z nepozornosti vyměnil pořadí číslic v jednom z činitelů a dostal součin, který byl o 4 248 menší než správný výsledek. Jaký je správný výsledek? Kolik mělo Karlovi správně vyjít?
Karel měl vynásobit dvě dvouciferná čísla. Z nepozornosti vyměnil pořadí číslic v jednom z činitelů a dostal součin, který byl o 4 248 menší než správný výsledek. Jaký je správný výsledek? Kolik mělo Karlovi správně vyjít? - Rozhodněte 82454
 Adam měl papír, který byl natolik velký, že by se z něj dalo natrhat několik desítek tisíc kousků. Nejprve papír roztrhal na čtyři kousky. Každý z těchto kousků vzal a roztrhal buď na čtyři, nebo na deset kousků. Stejným způsobem pokračoval dál: každý nov
Adam měl papír, který byl natolik velký, že by se z něj dalo natrhat několik desítek tisíc kousků. Nejprve papír roztrhal na čtyři kousky. Každý z těchto kousků vzal a roztrhal buď na čtyři, nebo na deset kousků. Stejným způsobem pokračoval dál: každý nov - V loňském
 V loňském roce bylo v našem skautském oddíle o 30 chlapců více než děvčat. Letos se počet dětí v oddíle zvětšil o 10% přičemž počet chlapců se zvětšil o 5% a počet děvčat se zvětšil o 20%. Kolik dětí máme letos v oddíle?
V loňském roce bylo v našem skautském oddíle o 30 chlapců více než děvčat. Letos se počet dětí v oddíle zvětšil o 10% přičemž počet chlapců se zvětšil o 5% a počet děvčat se zvětšil o 20%. Kolik dětí máme letos v oddíle? - Myslím 20
 Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím?
Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím? - Čtyřúhelníku 81469
 Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji
Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji
- Z6-I-3 2022
 Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním
Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním - Z7–I–5 MO 2022
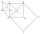 Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte...
Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte... - MO z7 2022
 Jsou také dva rovnostranné trojúhelníky ABC a BDE tak že velikost úhlu ABD je větší než 120° a menší než 180° bod C, E leží ve stejné polorovině vymezené přímkou AD. Průsečík CD a AE je označen F. Určete velikost úhlu AFD.
Jsou také dva rovnostranné trojúhelníky ABC a BDE tak že velikost úhlu ABD je větší než 120° a menší než 180° bod C, E leží ve stejné polorovině vymezené přímkou AD. Průsečík CD a AE je označen F. Určete velikost úhlu AFD. - Mo z9 2022 čtverce
 Vrcholy čtverce ABCD spojuje lomená čára DEFGHB. Menší úhly u vrcholů E, F, G, H jsou pravé a úsečky DE, EF, FG, GH, HB po řadě měří 6 cm, 4cm, 4 cm, 1 cm, 2 cm. Určete obsah čtverce ABCD.
Vrcholy čtverce ABCD spojuje lomená čára DEFGHB. Menší úhly u vrcholů E, F, G, H jsou pravé a úsečky DE, EF, FG, GH, HB po řadě měří 6 cm, 4cm, 4 cm, 1 cm, 2 cm. Určete obsah čtverce ABCD. - MO Z7 2022
 Eva si myslela dvě přirozená čísla. Tyto nejprve správně sečetla, poté správně odečetla. V obou případech dostala dvouciferný výsledek. Součin takto vzniklých dvouciferných čísel byl 645. Která čísla si Eva myslela? Prosím vás, jaký je tento výsledek?
Eva si myslela dvě přirozená čísla. Tyto nejprve správně sečetla, poté správně odečetla. V obou případech dostala dvouciferný výsledek. Součin takto vzniklých dvouciferných čísel byl 645. Která čísla si Eva myslela? Prosím vás, jaký je tento výsledek?
- Petra 3 MO 2022
 Petra měla napsaná přirozená čísla od 1 do 9. Dvě z těchto čísel sečetla, smazala a výsledný součet napsala místo sčítanců. Měla tak napsáno osm čísel, která se jí podařilo rozdělit do dvou skupin se stejným součinem. Určete jaký největší mohl být tento s
Petra měla napsaná přirozená čísla od 1 do 9. Dvě z těchto čísel sečetla, smazala a výsledný součet napsala místo sčítanců. Měla tak napsáno osm čísel, která se jí podařilo rozdělit do dvou skupin se stejným součinem. Určete jaký největší mohl být tento s - Polovina 80757
 Na louce bylo 45 ovcí a několik pastýřů. Poté, co z louky odešla polovina pastevců a třetina ovcí, měli zbylí pastevci a ovce celkem 126 nohou. Všechny ovce a všichni pastevci měli obvykle počty nohou. kolik pastýřů bylo původně na louce?
Na louce bylo 45 ovcí a několik pastýřů. Poté, co z louky odešla polovina pastevců a třetina ovcí, měli zbylí pastevci a ovce celkem 126 nohou. Všechny ovce a všichni pastevci měli obvykle počty nohou. kolik pastýřů bylo původně na louce? - MO Z7 2022 - Průměrný vek
 Průměrný věk dědy, babičky a jejich pěti vnoučat je 26 let. Průměrný věk samotných vnoučat je 7 let. Babička je o rok mladší než děda. Kolik let je babičce?
Průměrný věk dědy, babičky a jejich pěti vnoučat je 26 let. Průměrný věk samotných vnoučat je 7 let. Babička je o rok mladší než děda. Kolik let je babičce?
