4b jehlan
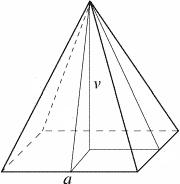
Pravidelný čtyřboký jehlan má podstavnou hranu a = 9, pobočnou hranu b = 44. Jakou má výšku?
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Vypočítej 391
 Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm
Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm - Věžička 2
 Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn
Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn - Šestiboký 6
 Šestiboký jehlan má obvod 120 cm, délku noční hrany 25 cm. Vypočítej jeho objem.
Šestiboký jehlan má obvod 120 cm, délku noční hrany 25 cm. Vypočítej jeho objem. - Stěnová výška
 Aký je objem pravidelného čtyřbokého jehlanu, výška jehlanu 30 cm a stěnová výška je 50 cm?
Aký je objem pravidelného čtyřbokého jehlanu, výška jehlanu 30 cm a stěnová výška je 50 cm? - Bukový
 Bukový školní model pravidelného čtyřbokého jehlanu má podstavou hranu dlouhou 20 cm a výšku 24 cm. Vypočítejte a) povrch jehlanu ve čtverečných decimetrech, b) hmotnost jehlanu v kilogramech, je-li hustota buku ρ=0,8g/cm³
Bukový školní model pravidelného čtyřbokého jehlanu má podstavou hranu dlouhou 20 cm a výšku 24 cm. Vypočítejte a) povrch jehlanu ve čtverečných decimetrech, b) hmotnost jehlanu v kilogramech, je-li hustota buku ρ=0,8g/cm³ - Pyramida
 Najděte celkový povrch obdélníkové pyramidy, má-li je vysoká 8 dm a základna je 10 dm x 6 dm.
Najděte celkový povrch obdélníkové pyramidy, má-li je vysoká 8 dm a základna je 10 dm x 6 dm. - Kolik 80
 Kolik litrů vody se vejde do ozdobné zahradní nádržky tvaru pravidelného šestibokého jehlanu s hranou podstavy délky 30 cm? Hloubka nádržky je 30 cm.
Kolik litrů vody se vejde do ozdobné zahradní nádržky tvaru pravidelného šestibokého jehlanu s hranou podstavy délky 30 cm? Hloubka nádržky je 30 cm. - Vypočítej 93
 Vypočítej povrch pravidelného čtyřbokého jehlanu, jestliže pro jeho objem V a tělesovou výšku v a podstavnou hranu a platí: V = 2,8 m³, v = 2,1 m
Vypočítej povrch pravidelného čtyřbokého jehlanu, jestliže pro jeho objem V a tělesovou výšku v a podstavnou hranu a platí: V = 2,8 m³, v = 2,1 m - Pravidelný 11
 Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu
Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu - Vypočítejte 49
 Vypočítejte objem V a povrch S pravidelného čtyřbokého jehlanu, jehož hrana podstavy i výška mají stejnou velikost jako hrana krychle o objemu V1=27m3
Vypočítejte objem V a povrch S pravidelného čtyřbokého jehlanu, jehož hrana podstavy i výška mají stejnou velikost jako hrana krychle o objemu V1=27m3 - Čtvercovou 46151
 Vypočítej povrch jehlanu se čtvercovou podstavou o hraně délky 6cm a výšce 6cm.
Vypočítej povrch jehlanu se čtvercovou podstavou o hraně délky 6cm a výšce 6cm. - Střecha
 Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²?
Střecha domu má tvar pravidelného čtyřbokého jehlanu o výšce 5 m a hraně podstavy 7 m. Kolik je třeba tašek o obsahu 540 cm²? - Potřebuji 44081
 Střecha v podobě jehlanu, na domě s půdorysem čtverce má rozměry 12 x 12 m, v nejvyšším bodě výšku 2m. Kolik krytiny potřebuji zakoupit? Počítej s rezervou 10%.
Střecha v podobě jehlanu, na domě s půdorysem čtverce má rozměry 12 x 12 m, v nejvyšším bodě výšku 2m. Kolik krytiny potřebuji zakoupit? Počítej s rezervou 10%. - Čtvercovou 44061
 Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška.
Jehlanová svíčka s čtvercovou podstavou má boční hranu s = 12 cm a hranu podstavy 4 cm. Kolik vosku budeme potřebovat k její výrobě a jak dlouhý knot, pokud je o 5% větší než její výška. - 4b jehlan 7
 Vypočítej povrch čtyřbokého jehlanu vysokého 3,5m s obdélníkovou podstavou s rozměry 3m a 1,8m.
Vypočítej povrch čtyřbokého jehlanu vysokého 3,5m s obdélníkovou podstavou s rozměry 3m a 1,8m. - Střecha
 Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem.
Střecha věže má tvar pravidelného čtyřbokého jehlanu, jehož podstavná hrana je dlouhá 11 m a boční stěna svírá s podstavou úhel velikosti 57°. Vypočtěte kolik krytiny potřebujeme na pokrytí celé střechy, pokud počítáme s 15% -ním odpadem.
