Z5–I–1 MO 2018
Míša má pět pastelek. Vojta jich má méně než Míša. Vendelín jich má tolik, kolik Míša a Vojta dohromady. Všichni tři dohromady mají sedmkrát více pastelek, než má Vojta.
Kolik pastelek má Vendelín?
Kolik pastelek má Vendelín?
Správná odpověď:

Zobrazuji 6 komentářů:
Dejv
resil jsem soustavou dvou rovnic m+v+× = 7v a x = m + v, pricemz m je 5 ze zadani a jako x jsem oznacil Vendelina, m Misu v Vojtu
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Z7–I–5 MO 2022
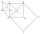 Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte...
Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte... - MO z7 2022
 Jsou také dva rovnostranné trojúhelníky ABC a BDE tak že velikost úhlu ABD je větší než 120° a menší než 180° bod C, E leží ve stejné polorovině vymezené přímkou AD. Průsečík CD a AE je označen F. Určete velikost úhlu AFD.
Jsou také dva rovnostranné trojúhelníky ABC a BDE tak že velikost úhlu ABD je větší než 120° a menší než 180° bod C, E leží ve stejné polorovině vymezené přímkou AD. Průsečík CD a AE je označen F. Určete velikost úhlu AFD. - Můj jediný
 Můj jediný syn se narodil když mi bylo 37 let. to bylo právě 32 let po smrti dědečka a ten zemřel ve svých 64 letech. Dedecek byl o 12 let starší než babička, brali se v roce 1947 právě když babičce bylo 18 let. V kterém roce se narodil můj syn?
Můj jediný syn se narodil když mi bylo 37 let. to bylo právě 32 let po smrti dědečka a ten zemřel ve svých 64 letech. Dedecek byl o 12 let starší než babička, brali se v roce 1947 právě když babičce bylo 18 let. V kterém roce se narodil můj syn?
- MO Z7–I–6 2021
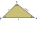 V trojúhelníku ABC leží na straně AC bod D a na straně BC bod E. Velikosti úhlů ABD, BAE, CAE a CBD jsou postupně 30°, 60°, 20° a 30°. určete velikost úhlu AED.
V trojúhelníku ABC leží na straně AC bod D a na straně BC bod E. Velikosti úhlů ABD, BAE, CAE a CBD jsou postupně 30°, 60°, 20° a 30°. určete velikost úhlu AED. - Přístavy MZ
 Mezi přístavy Mumraj a Zmatek pendlují po stejné trase dvě lodě. V přístavech tráví zanedbatelný čas, hned se otáčí a pokračují v plavbě. Ráno ve stejný okamžik vyplouvá modrá loď z přístavu Mumraj a zelená loď z přístavu Zmatek. Poprvé se lodě míjejí 20
Mezi přístavy Mumraj a Zmatek pendlují po stejné trase dvě lodě. V přístavech tráví zanedbatelný čas, hned se otáčí a pokračují v plavbě. Ráno ve stejný okamžik vyplouvá modrá loď z přístavu Mumraj a zelená loď z přístavu Zmatek. Poprvé se lodě míjejí 20 - Z6–I–5 MO 2019
 Útvar na obrázku vznikl tak, že z velkého kříže byl vystřižen malý kříž. Každý z těchto křížů může být složen z pěti shodných čtverců, přičemž strany malých čtverců jsou poloviční vzhledem ke stranám velkých čtverců. Obsah šedého útvaru na obrázku je 45 c
Útvar na obrázku vznikl tak, že z velkého kříže byl vystřižen malý kříž. Každý z těchto křížů může být složen z pěti shodných čtverců, přičemž strany malých čtverců jsou poloviční vzhledem ke stranám velkých čtverců. Obsah šedého útvaru na obrázku je 45 c - Z8–I–3 MO 2019
 Vendelín bydlí mezi dvěma zastávkami autobusu, a to ve třech osminách jejich vzdálenosti. Dnes vyrazil z domu a zjistil, že ať by utíkal k jedné, nebo druhé zastávce, dorazil by na zastávku současně s autobusem. Průměrná rychlost autobusu je 60 km/h. Jako
Vendelín bydlí mezi dvěma zastávkami autobusu, a to ve třech osminách jejich vzdálenosti. Dnes vyrazil z domu a zjistil, že ať by utíkal k jedné, nebo druhé zastávce, dorazil by na zastávku současně s autobusem. Průměrná rychlost autobusu je 60 km/h. Jako - C – I – 3 MO 2018
 Nechť a, b, c jsou kladná reálná čísla, jejichž součet je 3, a každé z nich je nejvýše 2. Dokažte, že platí nerovnost: a2 + b2 + c2 + 3abc < 9
Nechť a, b, c jsou kladná reálná čísla, jejichž součet je 3, a každé z nich je nejvýše 2. Dokažte, že platí nerovnost: a2 + b2 + c2 + 3abc < 9
- Z9 – I – 5 MO 2018
 Adam a Eva vytvářeli dekorace z navzájem shodných bílých kruhů. Adam použil čtyři kruhy, které sestavil tak, že se každý dotýkal dvou jiných kruhů. Mezi ně pak vložil jiný kruh, který se dotýkal všech čtyř bílých kruhů, a ten vybarvil červeně. Eva použila
Adam a Eva vytvářeli dekorace z navzájem shodných bílých kruhů. Adam použil čtyři kruhy, které sestavil tak, že se každý dotýkal dvou jiných kruhů. Mezi ně pak vložil jiný kruh, který se dotýkal všech čtyř bílých kruhů, a ten vybarvil červeně. Eva použila - Z7-1-3 MO 2018
 Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta
Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta - Z9 – I – 2 MO 2018
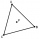 V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM.
V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Obdélníky 6598
 Adam měl tři shodné obdélníky. Přiložil je k sobě a dostal obdélník s obvodem 50 cm. Potom je přiložil jinak a dostal obdélník s větším obvodem. Vypoctej jeho obvod.
Adam měl tři shodné obdélníky. Přiložil je k sobě a dostal obdélník s obvodem 50 cm. Potom je přiložil jinak a dostal obdélník s větším obvodem. Vypoctej jeho obvod. - Z7-I-5 MO 2017
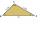 Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom
Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom
- Z9-I-5 MO 2017 obdélník
 Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC.
Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC. - Z7–I–2 MO 2017
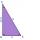 Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG.
Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG. - MO Z6–I–1 - 2017 - Anička
 Anička a Blanka si napsaly každá jedno dvojmístné číslo, které začínalo sedmičkou. Dívky si zvolily různá čísla. Poté každá mezi obě číslice vložila nulu, takže jim vzniklo trojmístné číslo. Od něj každá odečetla svoje původní dvojmístné číslo. Výsledek j
Anička a Blanka si napsaly každá jedno dvojmístné číslo, které začínalo sedmičkou. Dívky si zvolily různá čísla. Poté každá mezi obě číslice vložila nulu, takže jim vzniklo trojmístné číslo. Od něj každá odečetla svoje původní dvojmístné číslo. Výsledek j
