Cukrářka 2
Cukrářka potřebuje z cukrářské hmoty ve tvaru koule o poloměru 25cm vyřezat ozdobu ve tvaru kužele. Určete poloměr podstavy ozdoby a (a výšku h) tak, aby se na výrobu ozdoby použilo co nejvíce hmoty.
Správná odpověď:

Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- kvadratická rovnice
- vyjádření neznámé ze vzorce
- aritmetika
- druhá mocnina
- stereometrie
- kužel
- koule
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- základní funkce
- maximum
- derivace
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Poloha 2
 Poloha hmotného bodu, který se pohybuje podél osy x, je dána vztahem x=10t²-5t. Vyjádřete jeho rychlost a zrychlení.
Poloha hmotného bodu, který se pohybuje podél osy x, je dána vztahem x=10t²-5t. Vyjádřete jeho rychlost a zrychlení. - Spotřeba benzínu
 Spotřeba benzínu na kilometr M (jednotka kilometr na litr) auta Dodge Caliber je modelována funkcí M(s) = - 1/28s² + 3s- 31 Jakou má auto nejlepší spotřebu (benzinové kilometry) a jaké rychlosti dosáhne?
Spotřeba benzínu na kilometr M (jednotka kilometr na litr) auta Dodge Caliber je modelována funkcí M(s) = - 1/28s² + 3s- 31 Jakou má auto nejlepší spotřebu (benzinové kilometry) a jaké rychlosti dosáhne? - Na louce
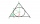 Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální?
Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální? - Megapizza
 Megapizza bude rozdělena mezi 100 lidí. 1. dostane 1%, 2. 2% ze zbytku, 3. 3% ze zbytku atd. Poslední 100. 100% ze zbytku. Který člověk dostal největší porci?
Megapizza bude rozdělena mezi 100 lidí. 1. dostane 1%, 2. 2% ze zbytku, 3. 3% ze zbytku atd. Poslední 100. 100% ze zbytku. Který člověk dostal největší porci? - Zaokrouhlenou 38351
 Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod
Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod - Rostoucí funcke
 Která z funkci je rostoucí? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
Která z funkci je rostoucí? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2 - Plášť 8
 Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální? - Střelec 4
 Střelec střílí do terče, přičemž předpokládáme, že jednotlivé výstřely jsou navzájem nezávislé a pravděpodobnost zásahu je u každého z nich 0,2. Střelec střílí tak dlouho, dokud poprvé terč nezasáhne, poté střelbu ukončí. (a) Jaký je nejpravděpodobnější p
Střelec střílí do terče, přičemž předpokládáme, že jednotlivé výstřely jsou navzájem nezávislé a pravděpodobnost zásahu je u každého z nich 0,2. Střelec střílí tak dlouho, dokud poprvé terč nezasáhne, poté střelbu ukončí. (a) Jaký je nejpravděpodobnější p - Derivační problém
 Součet dvou čísel je 12. Najděte tato čísla, jestliže: a) Součet jejich třetích mocnin je minimální. b) Součin jednoho s třetí mocninou druhého je maximální. c) Obě jsou kladná a součin jednoho s druhou mocninou druhého je maximální.
Součet dvou čísel je 12. Najděte tato čísla, jestliže: a) Součet jejich třetích mocnin je minimální. b) Součin jednoho s třetí mocninou druhého je maximální. c) Obě jsou kladná a součin jednoho s druhou mocninou druhého je maximální. - Simplexova metóda
 Řetězec obchodních domů plánuje investovat do televizní reklamy až 24 000 Eur. Všechny reklamní spoty budou umístěny na televizní stanici, na níž odvysílání 30 sekundového spotu stojí 1000 Eur a sleduje ho 14 000 potenciálních zákazníků, během prime týmu
Řetězec obchodních domů plánuje investovat do televizní reklamy až 24 000 Eur. Všechny reklamní spoty budou umístěny na televizní stanici, na níž odvysílání 30 sekundového spotu stojí 1000 Eur a sleduje ho 14 000 potenciálních zákazníků, během prime týmu - Tajný poklad
 Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad.
Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad. - Mimozemská loď
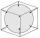 Mimozemská loď má tvar koule o poloměru r = 3000m a její posádka potřebuje lodí odvézt nasbíraný výzkumný materiál v boxu ve tvaru kvádru se čtvercovou podstavou. Určete délku podstavy a (a výšku h) tak, aby měl box největší možný objem.
Mimozemská loď má tvar koule o poloměru r = 3000m a její posádka potřebuje lodí odvézt nasbíraný výzkumný materiál v boxu ve tvaru kvádru se čtvercovou podstavou. Určete délku podstavy a (a výšku h) tak, aby měl box největší možný objem. - Vypočítejte: 8175
 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t - Vypočítejte: 8174
 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době - Vypočítejte: 8173
 Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t2; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného b
Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t2; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného b - Vypočítejte: 8172
 Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2s
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2s - Nejlevnější 7976
 V rekreační oblasti se má postavit bazén ve tvaru kvádru o objemu 200m³. Jeho délka má být 4-násobkem šířky, přičemž cena 1 m² dna bazénu je 2-krát levnější než 1 m² stěny bazénu. Jaké rozměry musí mít bazén, aby stavba byla nejlevnější?
V rekreační oblasti se má postavit bazén ve tvaru kvádru o objemu 200m³. Jeho délka má být 4-násobkem šířky, přičemž cena 1 m² dna bazénu je 2-krát levnější než 1 m² stěny bazénu. Jaké rozměry musí mít bazén, aby stavba byla nejlevnější?
