MO Z6–I–3 2018
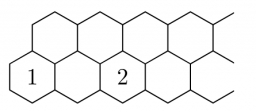
Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políčku v horní řadě.
Správný výsledek:
Správný výsledek:
Nejoblíbenější komentáře:
Ok
Je to jednoduché. 3 políčka, které se dotýkají musí mít součin 2018, tím pádem je jasný že dole mezi 1 a 2 bude 1009 a nahoře se tedy musí začít 2, jelikož se dotýká dolního políčka 1 a 1009 a pak se to pořád opakuje......
2019/3 je celé číslo, tím pádem víme, že hodnota toho čísla je hodnota, která je na 3. místě v horním řádku - tudíž 1009. Nevím, jestli to vysvětluje dobře, ale takhle to chápu já. :)
2019/3 je celé číslo, tím pádem víme, že hodnota toho čísla je hodnota, která je na 3. místě v horním řádku - tudíž 1009. Nevím, jestli to vysvětluje dobře, ale takhle to chápu já. :)
1 rok 5 Likes
Žák2
Dobrý den mohli by jste to napsat do těch šestiúhelníků prosím a těm výpočtům vůbec ale vůbec nechápu děkuji vám předem.
Ok
Je to jednoduché. 3 políčka, které se dotýkají musí mít součin 2018, tím pádem je jasný že dole mezi 1 a 2 bude 1009 a nahoře se tedy musí začít 2, jelikož se dotýká dolního políčka 1 a 1009 a pak se to pořád opakuje......
2019/3 je celé číslo, tím pádem víme, že hodnota toho čísla je hodnota, která je na 3. místě v horním řádku - tudíž 1009. Nevím, jestli to vysvětluje dobře, ale takhle to chápu já. :)
2019/3 je celé číslo, tím pádem víme, že hodnota toho čísla je hodnota, která je na 3. místě v horním řádku - tudíž 1009. Nevím, jestli to vysvětluje dobře, ale takhle to chápu já. :)
1 rok 5 Likes
Dr Math
Oficialni reseni:
Nápověda. Která čísla můžete doplňovat?
Možné řešení. Prvočíselný rozklad čísla 2018 je 2 · 1009. Číslo 2018 je tedy možné zapsat jako součin tří kladných čísel pouze dvěma způsoby (až na záměnu pořadí činitelů):
1 · 1 · 2018, 1 · 2 · 1009.
Do prázdných polí je tedy možno doplnit pouze některá z čísel 1, 2, 1009 a 2018. Kvůli snadnějšímu vyjadřování si neznámá čísla v prázdných polích označíme:
1
A
B
C
2
D
E
F
G
Aby platilo 1 · A · B = A · B · C, musí být C = 1. Aby platilo A · B · C = B · C · 2, musí být A = 2. Aby platilo B · C · 2 = C · 2 · D, musí být D = B. Takto postupně zjišťujeme 1 = C = E, A = 2 = F, B = D = G atd.
Čísla v polích se tedy pravidelně opakují podle následujícího vzoru:
1
2
B
1
2
B
1
2
B
1
Aby nyní součin libovolných tří navzájem sousedících polí byl 2018, musí být B = 1009. V horním řádku se tedy pravidelně střídá trojice čísel 2, 1, 1009. Jelikož 2019 = 3 · 673, je 2019. políčko třetím políčkem v 673. trojici v horním řádku. Proto je v tomto políčku číslo 1009.
Poznámka. Jakmile víme, která čísla se mohou v polích vyskytovat, můžeme je začít postupně doplňovat do některého z prázdných polí a následně zkoumat, zda a případně jak pokračovat dále. Tak lze vyloučit všechny možnosti až na tu uvedenou výše. (Kdybychom např. doplnili A = 1, potom z požadavku 1 · A · B = 2018 plyne, že B = 2018. Aby dále
platilo A · B · C = 2018, muselo by být C = 1, a tedy B · C · 2 = 2018 · 1 · 2. Tento součin však není 2018, proto A nemůže být 1.)
Řešení, ze kterého není patrné, proč výše uvedené doplnění je jediné možné, nemůže být hodnoceno nejlepším stupněm.
Nápověda. Která čísla můžete doplňovat?
Možné řešení. Prvočíselný rozklad čísla 2018 je 2 · 1009. Číslo 2018 je tedy možné zapsat jako součin tří kladných čísel pouze dvěma způsoby (až na záměnu pořadí činitelů):
1 · 1 · 2018, 1 · 2 · 1009.
Do prázdných polí je tedy možno doplnit pouze některá z čísel 1, 2, 1009 a 2018. Kvůli snadnějšímu vyjadřování si neznámá čísla v prázdných polích označíme:
1
A
B
C
2
D
E
F
G
Aby platilo 1 · A · B = A · B · C, musí být C = 1. Aby platilo A · B · C = B · C · 2, musí být A = 2. Aby platilo B · C · 2 = C · 2 · D, musí být D = B. Takto postupně zjišťujeme 1 = C = E, A = 2 = F, B = D = G atd.
Čísla v polích se tedy pravidelně opakují podle následujícího vzoru:
1
2
B
1
2
B
1
2
B
1
Aby nyní součin libovolných tří navzájem sousedících polí byl 2018, musí být B = 1009. V horním řádku se tedy pravidelně střídá trojice čísel 2, 1, 1009. Jelikož 2019 = 3 · 673, je 2019. políčko třetím políčkem v 673. trojici v horním řádku. Proto je v tomto políčku číslo 1009.
Poznámka. Jakmile víme, která čísla se mohou v polích vyskytovat, můžeme je začít postupně doplňovat do některého z prázdných polí a následně zkoumat, zda a případně jak pokračovat dále. Tak lze vyloučit všechny možnosti až na tu uvedenou výše. (Kdybychom např. doplnili A = 1, potom z požadavku 1 · A · B = 2018 plyne, že B = 2018. Aby dále
platilo A · B · C = 2018, muselo by být C = 1, a tedy B · C · 2 = 2018 · 1 · 2. Tento součin však není 2018, proto A nemůže být 1.)
Řešení, ze kterého není patrné, proč výše uvedené doplnění je jediné možné, nemůže být hodnoceno nejlepším stupněm.
Tipy na související online kalkulačky
Chcete převést dělení přirozených čísel - zjistit podíl a zbytek?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Další podobné příklady a úkoly:
- Číslice rozvoj
Určete, která číslice je na 1000. místě za desetinnou čárkou v desetinném rozvoji čísla 9/28 . - Čtvrthodina
Kdyby hodiny ukazovaly o čtvrthodinu více, bylo by na nich o 10minut 10 hodin. Kolik hodin ukazují? - Jestli 2
Jestli že predevčirem byla neděle jaký den v týdnu bude odedneška za 50 dní. (0 = pondelí, 6 = nedele) - Z5–I–4 MO 2019
Vojta začal vypisovat do sešitu číslo letošního školního roku 2019202020192020. . . A tak pokračoval pořád dál. Když napsal 2020 číslic, přestalo ho to bavit. Kolik tak napsal dvojek? - MO B 2019 ukol 2
Přirozené číslo n má aspoň 73 dvojmístných dělitelů. Dokažte, že jedním z nich je číslo 60. Uveďte rovněž příklad čísla n, které má právě 73 dvojmístných dělitelů, včetně náležitého zdůvodnění. - Elektřina - výpadek
V úterý v 6 hodin byla přerušena dodávka elektřiny na 156 h. Který den (1=pondeli, . .. 7 =nedele) a v kolik hodin byla dodávka elektřiny obnovena? - Veliké číslo
aký zbytek dává při dělení číslem 9 číslo 10 na 47 - 111? - Vánoce
Otec řekl. ,, Přesně o 56 hodin si sedneme k štědrovečernímu stolu. "Kolikátého bylo a kolik bylo hodin když tatínek řekl tuto větu? K štědrovečernímu stolu u nich sedají přesně o 18-té hodině. - Zvonkohra
Zvonkohra na nádvoří hraje v každou celou hodinu krátkou skladbu, a to počínaje 8. a konče 22. hodinou. Skladeb je celkem osmnáct, v celou hodinu se hraje vždy jen jedna a po odehrání všech osmnácti se začíná ve stejném pořadí znovu. Olga a Libor byli na - Babkine hodiny
Babkine hodiny se každou hodinu zpožďují o půl minuty. Babka jejich o 8,00 hod. nastaví přesně. Kolik budou hodiny ukazovat o 24 hod.? - Vánoce
Přesně o 76 hodin si sedneme k štědrovečernímu stolu. Kolikátého bylo a kolik bylo hodin když tatínek řekl tuto větu. K štědrovečernímu stolu u nich sedají přesně o 18-té hodině. - Zbytky
Daná je množina čísel { 170; 244; 299; 333; 351; 391; 423; 644 }. Dělte tato čísla číslem 66. Určete množinu zbytků a jako výsledek udejte součet těchto zbytků. - Rozděl bonbóny
Mamka koupila svým dětem balíček cukríkov.Všetkých 100 bonbónů z balíku rozdělila mezi svých 4 dětí tak, aby každé dítě dostalo co nejvíce a aby jí zůstalo co nejméně cukríkov. Koľko bonbónů zůstalo mamince. - Hodiny
Kolikrát za den se ručičky na hodinách překryjí? - RWY
Vypočtěte opačný směr dráhy 13. Přistávací dráhy jsou pojmenovány číslem mezi 01 a 36, který je jedna desetina azimutu dráhy ve stupních; dráha číslo 09 je východní (90°), dráha 18 je na jih (180°), dráha 27 bodů západ (270°) a dráha 36 je směrem sever (3 - Dělitelnost
Je číslo 237610 dělitelné číslem 5? - Hry s datem
Ať je dnes sobota. Jaký den bude o 71 dní? Výsledek zapište jako číslo: 1=pondělí, 2=úterý, 3=středa, 4=čtvrtek, 5=pátek, 6=sobota, 7=neděle?
