Asymptota
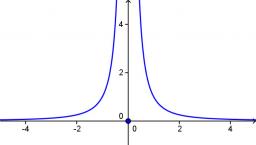
Určite vertikálnu asymptotu funkcie f(x)=2x+26−2x−8.
Správná odpověď:
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Přímka v prostoru
Dané jsou body A [1;a2;a3], B [3;-4;-1], C [-3;-1;8] . Body A, B, C leží na přímce. Vypočítej souradnice a2, a3 - Určete 50
Určete souřadnice vrcholu obdélníku vepsaneho do kružnice x²+y² -2x-4y-20=0, vite-li, že jedna jeho strana leží na přímce p: x+2y=0 - 9x^2−4y^2=36 82642
Napište rovnici tečny hyperboly 9x²−4y²=36 v bodě T =[t1,4]. - Vzdálenost 82341
Určete rovnici kružnice, která je množinou všech bodů roviny, které mají od bodu [3,7] dvakrát větší vzdálenost než od bodu [0,1]. - Oštěpařky
Oštěpařky Anna a Barbora mají průměrně délky hodů 67 m, respektive 75 m, a směrodatné odchylky 6 m, respektive 3 m. Předpokládejme, že délky hodů mají nezávislá normální rozdělení. Spočtěte pravděpodobnost, že při jednom hodu hodí Anna dál než Barbora. - Spotřeba benzínu
Spotřeba benzínu na kilometr M (jednotka kilometr na litr) auta Dodge Caliber je modelována funkcí M(s) = - 1/28s² + 3s- 31 Jakou má auto nejlepší spotřebu (benzinové kilometry) a jaké rychlosti dosáhne? - Užitím
Užitím periodičnosti zjednodušte cos 1125° - 1/2:x=5:3/4 81543
Vypočítej x v úměrech: x:7=6:4 1/2:x=5:3/4 4:3=8:x - Určete 45
Určete definiční obory funkcí: y=4/x (zápis ve zlomku) - Operace 4
Operace * (hviezdička) přiřazujíci dvěma dvojicím čísel jedno číslo je zavedena takto: (a, b)*(c, d) = ac+bd víme že: (x,2)*(-1, v) = -1 a (2,-1)*(u, v)=5 a (u, v)*(1,1)=-2 Čemu je rovno (1,2)*(x, y) jesliže y=3? - Na rovnici paraboly
V tenisovém zápase je Adrien 5 m od sítě, když odpálí míč vysoký 80 cm od země. Maximální výška jeho parabolické dráhy procházející přes síť byla 1,5 m . Pokud je délka kurtu je 23,77 m, dopadne míček dovnitř kurtu? - Poměr 44
Poměr množství tekutin k tuhým složkám stravy v (kg) má být asi 7:2. Znázorněte v pravoúhlé soustavě souřadnic závislost množství pevné složky stravy na jejím celkovém množství. - Proporcionální 74524
Která tabulka ukazuje proporcionální vztah mezi x a y? A) x 3 9 10 15 y 1 3 4 5 B) x 2 3 5 6 y 3 4 7 9 c) x 1 5 8 10 r 15 75 120 150 D) x 4 6 8 10 y 6 8 10 12 - Operace 3
Operace ♤ je definována vztahem A♤B = AB - A - B. Čemu se rovná hodnota výrazu 5♤(4♤3)? - Rovnice 39
Rovnice linearní funkcí je : y=-3x+4 a) urči průsečíky s osami načrtni graf b) pro které x platí f(x)=-1 c) pro které x platí f(x)=0 d) pro které y platí f(-1/2)=y - Odhadněte odmocninu
Odhadněte √38 s přesností na setiny pomocí kterékoli ze dvou metod (metoda dělení a průměru nebo vzorec pro odhad druhé odmocniny). - Experimentu 60823
Během vědeckého experimentu se kapalina zahřívala rychlostí 8 stupňů Celsia za minutu po dobu 10 minut. Potom se nechalo ztratit teplo rychlostí 6 stupňů Celsia za minutu. Pokud byla konečná teplota 76 stupňů Celsia, jaká byla teplota před 16 minutami?
