Vektory - základní operace
Dáno jsou body A [-11; 14] B [-1; -18] C[10; -20] a D[19; 15]
a. Určitě souřadnice vektorů u = AB v = CD s = DB
b. Vypočítejte vektorový součet u + v
c. Vypočítejte rozdíl vektorů u-v
d. Určitě souřadnice vektoru w = -4.u
a. Určitě souřadnice vektorů u = AB v = CD s = DB
b. Vypočítejte vektorový součet u + v
c. Vypočítejte rozdíl vektorů u-v
d. Určitě souřadnice vektoru w = -4.u
Správná odpověď:
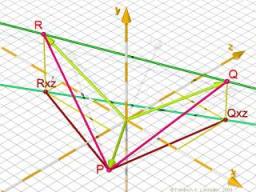
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Vektor
 Určitě souřadnice vektoru u=CD, když C[-18;17], D[7,9].
Určitě souřadnice vektoru u=CD, když C[-18;17], D[7,9]. - 4)]-{-28-41•[-8•2+4•1•(0 34791
 Vypočítejte příklad s desetinnými čísly: -5+(-14+11)•[24-2•(-0,4)]-{-28-41•[-8•2+4•1•(0,1-2,4)]+ 1}=
Vypočítejte příklad s desetinnými čísly: -5+(-14+11)•[24-2•(-0,4)]-{-28-41•[-8•2+4•1•(0,1-2,4)]+ 1}= - Jednotkový vektor
 Zjistěte jednotkový vektor (jeho souřadnice) k vektoru AB pokud A[-4; 18], B[-12; -13].
Zjistěte jednotkový vektor (jeho souřadnice) k vektoru AB pokud A[-4; 18], B[-12; -13]. - Čtyřboký jehlan
 Je dán pravidelný čtyřboký jehlan ABCDV; | AB | = 4cm; v = 6cm. Určete úhel přímek AD a BV.
Je dán pravidelný čtyřboký jehlan ABCDV; | AB | = 4cm; v = 6cm. Určete úhel přímek AD a BV. - Těžiště
 Hmotné body jsou rozloženy v prostoru následovně - zadané souřadnice v prostoru a jejich hmotnosti. Najděte polohu těžiště této soustavy hmotných bodů: A1 [4; -15; -20] m1 = 12 kg A2 [-4; 17; -6] m2 = 51 kg A
Hmotné body jsou rozloženy v prostoru následovně - zadané souřadnice v prostoru a jejich hmotnosti. Najděte polohu těžiště této soustavy hmotných bodů: A1 [4; -15; -20] m1 = 12 kg A2 [-4; 17; -6] m2 = 51 kg A - Souřadnice těžiště
 Nechť A = [3, 2, 0], B = [1, -2, 4] a C = [1, 1, 1] jsou 3 body v prostoru. Vypočítejte souřadnice těžiště △ ABC (je to průsečík těžnic).
Nechť A = [3, 2, 0], B = [1, -2, 4] a C = [1, 1, 1] jsou 3 body v prostoru. Vypočítejte souřadnice těžiště △ ABC (je to průsečík těžnic). - Těžiště
 Vypočítejte souřadnice těžiště T [x, y] trojúhelníku ABC; A[1,19] B[5,-9] C[17,12]
Vypočítejte souřadnice těžiště T [x, y] trojúhelníku ABC; A[1,19] B[5,-9] C[17,12] - Vektorový součet
 Velikost vektoru u je 4, vektoru v je 10. Vektory svírají úhel 60 °. Jaká je velikost vektoru u + v?
Velikost vektoru u je 4, vektoru v je 10. Vektory svírají úhel 60 °. Jaká je velikost vektoru u + v? - Úsečka
 Úsečka je dána dvěma body L [-10, -14] a M [-13, -4]. Vypočítejte souřadnice bodu na úsečce, který leží v 3/4 vzdálenosti mezi L a M.
Úsečka je dána dvěma body L [-10, -14] a M [-13, -4]. Vypočítejte souřadnice bodu na úsečce, který leží v 3/4 vzdálenosti mezi L a M. - Kružnice
 Z rovnice kružnice: 3x² +3y² +54x +168 = 0 Vypočítejte souřadnice středu kružnice S [x0, y0] a poloměr kružnice r.
Z rovnice kružnice: 3x² +3y² +54x +168 = 0 Vypočítejte souřadnice středu kružnice S [x0, y0] a poloměr kružnice r. - 3)+3•[14-(23-4•5)]-2•{36-[18-(28-76)]}= 34731
 Vyhodnoťte výraz se závorkami: 12•(-4,3)+3•[14-(23-4•5)]-2•{36-[18-(28-76)]}=
Vyhodnoťte výraz se závorkami: 12•(-4,3)+3•[14-(23-4•5)]-2•{36-[18-(28-76)]}= - Osová souměrnost
 Vypočítejte souřadnice bodu B osově symetricky s bodem A [-1, -3] podél přímky p: x + y - 2 = 0.
Vypočítejte souřadnice bodu B osově symetricky s bodem A [-1, -3] podél přímky p: x + y - 2 = 0. - Následujícímu 57921
 Která volba NENÍ ekvivalentní následujícímu výrazu? 9 x { [ 14 ÷ 2 + (4-1) ] - 8 } A 9 x { 10 - 8 } B 9 x { [ 14 ÷ 2 + 3] - 8 } C 9 x 10 – 8 D 18
Která volba NENÍ ekvivalentní následujícímu výrazu? 9 x { [ 14 ÷ 2 + (4-1) ] - 8 } A 9 x { 10 - 8 } B 9 x { [ 14 ÷ 2 + 3] - 8 } C 9 x 10 – 8 D 18 - Souřadnice vektoru
 Určete souřadnice vektoru u = CD, pokud C (19; -7) a D (-16; -5)
Určete souřadnice vektoru u = CD, pokud C (19; -7) a D (-16; -5) - Úsečka
 Vypočítejte délku úsečky AB, jestliže souřadnice koncových bodů jsou A[5, -6] a B[-5, -2].
Vypočítejte délku úsečky AB, jestliže souřadnice koncových bodů jsou A[5, -6] a B[-5, -2]. - Vypočítejte: 72474
 Vypočítejte: A) 6/14 + 1/14 = B) 1 2/5 + 2 1/5 = C) 2/13 + 5/13 + 7/13 = D) 2 1/10 + 0/10 = E) 3 + 10/11 = F) 2/3 + 4/3 = 7/5 + 6/5 = G) 4 1/9 + 2 4/9 = H) 8 3/8 + 3 1/8 + 1 7/8 = I) 4/9 + 6 1/9 = J) 11/6 + 2 1/6 = K) 0 1/15 + 7/15 + 3 4/15 =
Vypočítejte: A) 6/14 + 1/14 = B) 1 2/5 + 2 1/5 = C) 2/13 + 5/13 + 7/13 = D) 2 1/10 + 0/10 = E) 3 + 10/11 = F) 2/3 + 4/3 = 7/5 + 6/5 = G) 4 1/9 + 2 4/9 = H) 8 3/8 + 3 1/8 + 1 7/8 = I) 4/9 + 6 1/9 = J) 11/6 + 2 1/6 = K) 0 1/15 + 7/15 + 3 4/15 = - Parabola
 Najděte rovnici paraboly, která obsahuje body A[9; 8], B[13; 1], C[16; -10]. (použite y = ax² + bx + c)
Najděte rovnici paraboly, která obsahuje body A[9; 8], B[13; 1], C[16; -10]. (použite y = ax² + bx + c)
