Sladkosti
3 čokolády a 7 zákusků stojí 85,- Kč. 6 čokolád a 2 zákusky stojí 86,- Kč. Kolik stojí 5 čokolád a 9 zákusků?
Zajímalo by nás, jak dojít k výsledku, ale jen logickou úvahou bez užití soustavy rovnic
Zajímalo by nás, jak dojít k výsledku, ale jen logickou úvahou bez užití soustavy rovnic
Správná odpověď:

Zobrazuji 1 komentář:
Www
Co se tyce reseni uvahou me nic zatim nenapada; da se vsak simulovat reseni soustavy rovnic, napr. z druhej vety vyplyva, ze 1 zakusek stoji 43 Kc minus 3 cokolady. Dosadite do prvej vety a mate cenu 1 cokolady. Ci je to uvaha nebo reseni rovnic, je to ekvivalentni.
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Prázdne pokoje
 V turistické ubytovně spalo 44 žáků v osmi pokojích, některé byly čtyřlůžkové, jiné šesti lůžkové, Kolik čtyřlůžkových a kolík šesti lůžkových pokojů bylo v ubytovně, když dvě lůžka byla prázdná?
V turistické ubytovně spalo 44 žáků v osmi pokojích, některé byly čtyřlůžkové, jiné šesti lůžkové, Kolik čtyřlůžkových a kolík šesti lůžkových pokojů bylo v ubytovně, když dvě lůžka byla prázdná? - Číslo 40
 Číslo 112 rozděl na tři složky x, y, z tak, aby platilo x : y = 7 : 5 a y : z = 3 : 4.
Číslo 112 rozděl na tři složky x, y, z tak, aby platilo x : y = 7 : 5 a y : z = 3 : 4. - Ovoce 7
 Cena 6 kg hrušek je o 77 Kč vyšší než cena 5 kg jablek. Cena 6 kg jablek je stejná jako cena 5 kg hrušek. Kolik stojí 2 kg jablek?
Cena 6 kg hrušek je o 77 Kč vyšší než cena 5 kg jablek. Cena 6 kg jablek je stejná jako cena 5 kg hrušek. Kolik stojí 2 kg jablek? - V trojúhelníku 9
 V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
V trojúhelníku ABC je velikost vnitřního úhlu beta dvojnásobkem velikosti úhlu alfa a velikosti úhlu gama je o 20 stupňů menší než velikost úhlu beta. Urči velikost všech vnitřních úhlů tohoto trojúhelníku.
- Košíkář
 Košíkář prodal během prvních dvou dnů velikonoční trhu všechny upletene pomlazky, první den prodal pětinu všech pomlázek. Druhy den prodal o 180 pomlazek více než první den. Kolik pomlazek prodal kosikar první den velikonočních trhu?
Košíkář prodal během prvních dvou dnů velikonoční trhu všechny upletene pomlazky, první den prodal pětinu všech pomlázek. Druhy den prodal o 180 pomlazek více než první den. Kolik pomlazek prodal kosikar první den velikonočních trhu? - V koloně
 V koloně před mýtnou bránou stojí osobní auta a nákladní auta. Nákladní vůz je třikrát delší než osobní auto. Vypočítej, kolik stojí před autem, které právě přijelo, osobních aut, když je mezi nimi i jeden nákladní vůz, který tvoří jednu osminu délky fron
V koloně před mýtnou bránou stojí osobní auta a nákladní auta. Nákladní vůz je třikrát delší než osobní auto. Vypočítej, kolik stojí před autem, které právě přijelo, osobních aut, když je mezi nimi i jeden nákladní vůz, který tvoří jednu osminu délky fron - Obdélníku 83176
 Pokud zmenšíme délku obdélníku o 2cm a šířku o 1cm, tak se obsah obdélníku zmenší o 8 cm². Pokud zvětšíme délku obdélníku o 1cm a šířku o 2cm, tak se obsah obdélníku zvětší o 13 cm². Jaké byly původní rozměry obdélníku?
Pokud zmenšíme délku obdélníku o 2cm a šířku o 1cm, tak se obsah obdélníku zmenší o 8 cm². Pokud zvětšíme délku obdélníku o 1cm a šířku o 2cm, tak se obsah obdélníku zvětší o 13 cm². Jaké byly původní rozměry obdélníku? - V zeleném
 V zeleném kanystru bylo ráno o 6 litrů více než v modrém. Odpoledne zahradník 1 litr vody ze zeleného kanystru do modrého. v zeleném kanystru pak bylo dvakrát více vody než v modrém. Kolik bylo ráno v zeleném kanystru. Kolik bylo v obou dohromady.
V zeleném kanystru bylo ráno o 6 litrů více než v modrém. Odpoledne zahradník 1 litr vody ze zeleného kanystru do modrého. v zeleném kanystru pak bylo dvakrát více vody než v modrém. Kolik bylo ráno v zeleném kanystru. Kolik bylo v obou dohromady. - Jedničku 83149
 Ve třídě je 30 žáků. Pět měli známku trojku. Ostatní dvojky a jednotky. Průměr známek byl 1,9. Kolik žáků mělo jedničku?
Ve třídě je 30 žáků. Pět měli známku trojku. Ostatní dvojky a jednotky. Průměr známek byl 1,9. Kolik žáků mělo jedničku?
- Knihomol
 Ondra četl knihu. První den přečetl jednu desetinu. Druhý den polovinu zbytku, třetí den 20% nového zbytku a čtvrtý den dočetl 72 zbývajících stran. Kolik stran měla kniha?
Ondra četl knihu. První den přečetl jednu desetinu. Druhý den polovinu zbytku, třetí den 20% nového zbytku a čtvrtý den dočetl 72 zbývajících stran. Kolik stran měla kniha? - Z6–I–5 MO 2024
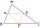 Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru
Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru - Sešity 2
 Jana koupila celkem 36 sešitů, přičemž linkovaných koupila třikrát více než čtverečkovaných. Vypočtěte, kolik linkovaných sešitů koupila.
Jana koupila celkem 36 sešitů, přičemž linkovaných koupila třikrát více než čtverečkovaných. Vypočtěte, kolik linkovaných sešitů koupila. - Chemické výpočty
 50% roztok soli je třeba naředit destilovanou vodou tak, aby vzniklo 20 litrů 35% roztoku. Kolik litrů původního roztoku a kolik litrů vody potřebujeme?
50% roztok soli je třeba naředit destilovanou vodou tak, aby vzniklo 20 litrů 35% roztoku. Kolik litrů původního roztoku a kolik litrů vody potřebujeme? - Jana koupila
 Jana koupila v papírnictví několik stejných linkovaných sešitů, několik stejných čtverečkovaných sešitů a několik stejných kružítek. Dva linkované sešity a dva čtverečkované sešity stojí dohromady 180 korun. Dva čtverečkované sešity stojí stejně jako tři
Jana koupila v papírnictví několik stejných linkovaných sešitů, několik stejných čtverečkovaných sešitů a několik stejných kružítek. Dva linkované sešity a dva čtverečkované sešity stojí dohromady 180 korun. Dva čtverečkované sešity stojí stejně jako tři
- Celý film
 Celý film trvá 1 hodinu. Doba, která ještě zbývá do konce filmu, je polovinou doby, která již uplynula od začátku filmu. Vypočtěte, kolik minut zbývá do konce filmu.
Celý film trvá 1 hodinu. Doba, která ještě zbývá do konce filmu, je polovinou doby, která již uplynula od začátku filmu. Vypočtěte, kolik minut zbývá do konce filmu. - Hrušky a jablká
 Víme, že 7kg jablek a 4kg hrušek koupila paní Havelková za 295 Kč. Podle pokladniho dokladu bylo možné zjistit, že 6kg jablek a 5kg hrušek bylo možné koupit za stejnou částku peněz. Určete cenu 1kg kupovanych jablek a 1kg kupovanych hrušek.
Víme, že 7kg jablek a 4kg hrušek koupila paní Havelková za 295 Kč. Podle pokladniho dokladu bylo možné zjistit, že 6kg jablek a 5kg hrušek bylo možné koupit za stejnou částku peněz. Určete cenu 1kg kupovanych jablek a 1kg kupovanych hrušek. - Mince 11
 K vyplaceni částky 570,-Kč pokladní použila 15 mincí: několik padesatikorun a několik dvacetikoruna. Jak částku vyplatila?
K vyplaceni částky 570,-Kč pokladní použila 15 mincí: několik padesatikorun a několik dvacetikoruna. Jak částku vyplatila?
