Sestroj
Sestroj trojúhelník ABC, a = 7 cm, b = 9 cm, pravý úhel u vrcholu C, sestroj osy všech tří stran. Odmerajte a zapíšte délku strany c.
Správná odpověď:
Zobrazuji 1 komentář:
Petr
Postup konstrukce:
1.nakreslis pravy uhol,
2. na jedno rameno uhla vyneseies kruzitkem usecku dlzky 7
3. na druhe rameno uhla vyneseies kruzitkem usecku dlzky 9
4. Vyznacis prusecniky ako body A, B
5. narysujes preponu AB
1.nakreslis pravy uhol,
2. na jedno rameno uhla vyneseies kruzitkem usecku dlzky 7
3. na druhe rameno uhla vyneseies kruzitkem usecku dlzky 9
4. Vyznacis prusecniky ako body A, B
5. narysujes preponu AB
8 let 2 Likes
Tipy na související online kalkulačky
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Chcete proměnit jednotky času, např. hodiny na minuty?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Chcete proměnit jednotky času, např. hodiny na minuty?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- geometrie
- Thaletova věta
- aritmetika
- odmocnina
- planimetrie
- pravoúhlý trojúhelník
- trojúhelník
- základní funkce
- procenta
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Těžnice 10
 Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°.
Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°. - Je dán 19
 Je dán čtverec ABCD 4,2 cm. Sestroj množinu všech bodů, které mají od některého z vrcholů vzdálenost menší nebo rovnu 2 cm a zároveň leží uvnitř tohoto čtverce . Uveď v procentech, jak velkou část čtverce tato oblast zabírá.
Je dán čtverec ABCD 4,2 cm. Sestroj množinu všech bodů, které mají od některého z vrcholů vzdálenost menší nebo rovnu 2 cm a zároveň leží uvnitř tohoto čtverce . Uveď v procentech, jak velkou část čtverce tato oblast zabírá. - Trojúhelník 73464
 Daná je úsečka BC délky 6cm. Sestroj trojúhelník tak, aby úhel BAC měl velikost 50° a výška na stranu a měla 5,5 cm. Děkuji pěkně.
Daná je úsečka BC délky 6cm. Sestroj trojúhelník tak, aby úhel BAC měl velikost 50° a výška na stranu a měla 5,5 cm. Děkuji pěkně. - Sestroj 21
 Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek.
Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek.
- Na úsečku
 Na úsečku narysuj bod x, ktery ji rozdelí v danem poměru: a) 2:3 b) 1:5 c) 6:2
Na úsečku narysuj bod x, ktery ji rozdelí v danem poměru: a) 2:3 b) 1:5 c) 6:2 - Sestrojte 9
 Sestrojte lichoběžník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A velikost úhlu ABC=60°
Sestrojte lichoběžník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A velikost úhlu ABC=60° - Sestroj 19
 Sestroj pravoúhlý trojúhelník ABC s přeponou AB: a) |AB|=72 mm, |BC|=51 mm b) |AB|=58 mm, |AC|= 42 mm
Sestroj pravoúhlý trojúhelník ABC s přeponou AB: a) |AB|=72 mm, |BC|=51 mm b) |AB|=58 mm, |AC|= 42 mm - Rovnoběžník 62084
 Rovnoběžník OPRS se stranou OP dlouhou 4 cm, stranou OS dlouhou 5 cm, úhel při vrcholu P má 100°. Jaký má obsah?
Rovnoběžník OPRS se stranou OP dlouhou 4 cm, stranou OS dlouhou 5 cm, úhel při vrcholu P má 100°. Jaký má obsah? - Trojúhelník 61854
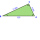 Sestroj trojúhelník ABC, je-li dáno a+b+c (obvod), výška na stranu c a úhel gama.
Sestroj trojúhelník ABC, je-li dáno a+b+c (obvod), výška na stranu c a úhel gama.
- Lichoběžník 61394
 Sestroj lichoběžník ABCD, pokud a=8cm, b=5cm, alfa=60°, beta = 75°
Sestroj lichoběžník ABCD, pokud a=8cm, b=5cm, alfa=60°, beta = 75° - Kosotvůrec 61354
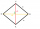 Sestrojte kosotvůrec ABCD se stranou a=4,8cm a úhel při vrcholu B má velikost 60°
Sestrojte kosotvůrec ABCD se stranou a=4,8cm a úhel při vrcholu B má velikost 60° - Euklidovy 61253
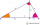 Pomocí Euklidovy věty sestrojte úsečku o délce √15.
Pomocí Euklidovy věty sestrojte úsečku o délce √15. - Sestroj 16
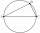 Sestroj pravoúhlý trojúhelník MNO, prepona o = 5 cm, úhel MNO = 37°
Sestroj pravoúhlý trojúhelník MNO, prepona o = 5 cm, úhel MNO = 37° - Jak sestrojit
 Jak sestrojit obdelnik pouze za pomoci kruznic
Jak sestrojit obdelnik pouze za pomoci kruznic
- Čtvercové 58873
 Narýsuj čtverec tak aby jeho strany neležely na čarách čtvercové sítě
Narýsuj čtverec tak aby jeho strany neležely na čarách čtvercové sítě - Písmena
 Zjistěte, která písmena (velká tiskací) lze napsat jako středově souměrná.
Zjistěte, která písmena (velká tiskací) lze napsat jako středově souměrná. - Rovnostranný 56651
 Rozdělte úsečku AB na tři stejné části. Návod: Sestrojte rovnostranný trojúhelník ABC a najděte jeho střed (např. popsané kružnice).
Rozdělte úsečku AB na tři stejné části. Návod: Sestrojte rovnostranný trojúhelník ABC a najděte jeho střed (např. popsané kružnice).
