Mirek a Zuzka
Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3.
Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich má pravdu.
Výsledek
Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich má pravdu.
Výsledek

Zobrazuji 1 komentář:
Mo-radca
Nápověda. Zjistěte, které různé součty lze získat.
Možné řešení. Všechny možné dvojice, které lze z daných čísel složit, jsou (1,1); (1,2),(2,1); (1,3),(2,2),(3,1); (2,3),(3,2); (3,3).
Tyto možnosti dávají 5 různých součtů, a to 2, 3, 4, 5, 6 (dvojice s různými součty jsou odděleny středníky). Na uvedeném obrázku však potřebujeme 6 dvojic s různými součty, pravdu má tedy Zuzka.
Poznámky.
a) K určení možných součtů není třeba vypisovat všechny přípustné dvojice:
nejmenší součet odpovídá 1 + 1 = 2, největší je 3 + 3 = 6. Odtud plyne, že možných součtů není víc než 5, což je méně než požadovaných 6.
b) Řešení úlohy pomocí všech možných vyplnění tabulky a kontrolou takto získaných součtů je extrémně pracné. Pokud by však takové řešení bylo úplné, nechť je považováno za správne.
Možné řešení. Všechny možné dvojice, které lze z daných čísel složit, jsou (1,1); (1,2),(2,1); (1,3),(2,2),(3,1); (2,3),(3,2); (3,3).
Tyto možnosti dávají 5 různých součtů, a to 2, 3, 4, 5, 6 (dvojice s různými součty jsou odděleny středníky). Na uvedeném obrázku však potřebujeme 6 dvojic s různými součty, pravdu má tedy Zuzka.
Poznámky.
a) K určení možných součtů není třeba vypisovat všechny přípustné dvojice:
nejmenší součet odpovídá 1 + 1 = 2, největší je 3 + 3 = 6. Odtud plyne, že možných součtů není víc než 5, což je méně než požadovaných 6.
b) Řešení úlohy pomocí všech možných vyplnění tabulky a kontrolou takto získaných součtů je extrémně pracné. Pokud by však takové řešení bylo úplné, nechť je považováno za správne.
8 let 2 Likes
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Z9–I–4 MO 2017
 Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p - Vláček
 Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakem. Vlak měl tři vagony a v každém se vezla právě tři čísla. Číslo 1 se vezlo v prvním vagonu a v posledním vagonu byla všechna čísla lichá. Průvodčí cestou spočítal součet čísel v prvním, druhém i posledním vagonu
Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakem. Vlak měl tři vagony a v každém se vezla právě tři čísla. Číslo 1 se vezlo v prvním vagonu a v posledním vagonu byla všechna čísla lichá. Průvodčí cestou spočítal součet čísel v prvním, druhém i posledním vagonu - C–I–4 MO 2017
 Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla.
Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla. - Na papíře
 Na papíře bylo napsáno několik kladných celých čísel. Miška si pamatovala pouze to, že každé číslo bylo polovinou součtu všech ostatních čísel. Kolik čísel mohlo být napsaných na papíře?
Na papíře bylo napsáno několik kladných celých čísel. Miška si pamatovala pouze to, že každé číslo bylo polovinou součtu všech ostatních čísel. Kolik čísel mohlo být napsaných na papíře? - Pyramida Z8–I–6
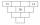 Každá cihlička následující pyramidy obsahuje jedno číslo. Kdykoli to je možné, je číslo v každé cihličce nejmenším společným násobkem čísel ze dvou cihliček ležících přímo na ní. Které číslo může být v nejspodnější cihličce? Určete všechny možnosti.
Každá cihlička následující pyramidy obsahuje jedno číslo. Kdykoli to je možné, je číslo v každé cihličce nejmenším společným násobkem čísel ze dvou cihliček ležících přímo na ní. Které číslo může být v nejspodnější cihličce? Určete všechny možnosti. - Fourland 3542
 V zemi Fourland mají pouze čtyři písmena F, O, U, R a každé slovo má právě čtyři písmena. V žádném slově se nesmí opakovat ani jedno písmeno. Napiš všechna slova, která se dají u nich napsat.
V zemi Fourland mají pouze čtyři písmena F, O, U, R a každé slovo má právě čtyři písmena. V žádném slově se nesmí opakovat ani jedno písmeno. Napiš všechna slova, která se dají u nich napsat. - Vnučka
 V roce 2014 byl součet věku Mecháčovy tety, její dcery a její vnučky roven 100 let. V kterém roce se narodila vnučka, pokud víme, že věk každé z nich lze vyjádřit jako mocnina dvou?
V roce 2014 byl součet věku Mecháčovy tety, její dcery a její vnučky roven 100 let. V kterém roce se narodila vnučka, pokud víme, že věk každé z nich lze vyjádřit jako mocnina dvou? - Z7–I–6, výstava koček
 Na výstavě dlouhosrstých koček se sešlo celkem deset vystavujících. Vystavovalo se v obdélníkové místnosti, ve které byly dvě řady stolů jako na obrázku. Kočky byly označeny navzájem různými čísly v rozmezí 1 až 10 a na každém stole seděla jedna kočka. Ur
Na výstavě dlouhosrstých koček se sešlo celkem deset vystavujících. Vystavovalo se v obdélníkové místnosti, ve které byly dvě řady stolů jako na obrázku. Kočky byly označeny navzájem různými čísly v rozmezí 1 až 10 a na každém stole seděla jedna kočka. Ur - Skupina
 Skupina 10 děvčat se má rozdělit na dvě skupiny tak, aby v každé byli nejméně 4 děvčata. Kolika způsoby to lze provést?
Skupina 10 děvčat se má rozdělit na dvě skupiny tak, aby v každé byli nejméně 4 děvčata. Kolika způsoby to lze provést? - MO Z6–I–3 2018
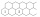 Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políč
Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políč - Z7–I–1 MO 2018
 Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné číslo poskládané z těchto kartiček je dělitelné šesti. Navíc lze z těchto kartiček poskládat trojmístné číslo
Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné číslo poskládané z těchto kartiček je dělitelné šesti. Navíc lze z těchto kartiček poskládat trojmístné číslo - Pozemek 10
 Pozemek pana Častky má rozměry 252 dm a 28 m. Jak nejdále od sebe musí rozmístit kůly na plot, aby byly po obou stranách stejně daleko? Kolik jich bude potřebovat na oplocení celého pozemku?
Pozemek pana Častky má rozměry 252 dm a 28 m. Jak nejdále od sebe musí rozmístit kůly na plot, aby byly po obou stranách stejně daleko? Kolik jich bude potřebovat na oplocení celého pozemku? - MO Z6-6-1
 Do prázdných polí v následujícím obrázku doplňte celá čísla větší než 1 tak, aby v každém tmavším políčku byl součin čísel ze sousedních světlejších políček: Jaké je číslo je středu?
Do prázdných polí v následujícím obrázku doplňte celá čísla větší než 1 tak, aby v každém tmavším políčku byl součin čísel ze sousedních světlejších políček: Jaké je číslo je středu? - Číselna osa
 V kocourkovské škole používají zvláštní číselnou osu. Vzdálenost mezi čísly 1 a 2 je 1 cm, vzdálenost mezi čísly 2 a 3 je 3 cm, mezi čísly 3 a 4 je 5 cm, a tak dále, vzdálenost mezi následující dvojicí přirozenými čísly se vždy zvètší o 2 cm. Mezi kterými
V kocourkovské škole používají zvláštní číselnou osu. Vzdálenost mezi čísly 1 a 2 je 1 cm, vzdálenost mezi čísly 2 a 3 je 3 cm, mezi čísly 3 a 4 je 5 cm, a tak dále, vzdálenost mezi následující dvojicí přirozenými čísly se vždy zvètší o 2 cm. Mezi kterými - Kupky
 Anička má celkem 702 Kč. Peníze musí rozdělit na různý počet kupek tak, aby na každé kupce byl stejný počet Kč. Kolik má možností?
Anička má celkem 702 Kč. Peníze musí rozdělit na různý počet kupek tak, aby na každé kupce byl stejný počet Kč. Kolik má možností? - MO Z6-1-3 2017 šachovnica
 Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H
Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H - Pan Cuketa
 Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja
Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja
