Řezy koule
V jaké vzdálenosti od středu protíná kouli o poloměru R = 56 rovina, jestliže obsah řezu a obsah hlavního kruhu je v poměru 1/2.
Správná odpověď:
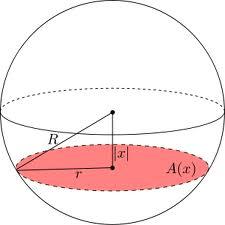
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Rohy krychle
 Z krychle o hraně 6 cm odřízneme všechny vrcholy tak, že každá rovina řezu protíná hrany 2 cm od nejbližšího vrcholu. Kolik hran bude mít toto těleso?
Z krychle o hraně 6 cm odřízneme všechny vrcholy tak, že každá rovina řezu protíná hrany 2 cm od nejbližšího vrcholu. Kolik hran bude mít toto těleso? - Tětiva 3
 Jaký poloměr má kružnice, jestliže její tětiva je vzdálená od středu o 2/3 poloměru a má délku 10cm?
Jaký poloměr má kružnice, jestliže její tětiva je vzdálená od středu o 2/3 poloměru a má délku 10cm? - Tětiva kružnice
 Vypočítejte délku tětivy kružnice o poloměru r = 10 cm, jejíž délka se rovná její vzdálenosti od středu kružnice.
Vypočítejte délku tětivy kružnice o poloměru r = 10 cm, jejíž délka se rovná její vzdálenosti od středu kružnice. - Odsek úseče
 Od koule k o poloměru r=1 je odseknuta taková úseč, že objem koule vepsané do této úseče je roven 1/6 objemu úseče. Jaká je vzdálenost sečné roviny od středu koule k?
Od koule k o poloměru r=1 je odseknuta taková úseč, že objem koule vepsané do této úseče je roven 1/6 objemu úseče. Jaká je vzdálenost sečné roviny od středu koule k? - Proťatá koule
 Vypočítejte objem a povrch koule, jestliže poloměry rovnoběžných řezů jsou r1=64 cm, r2=57 cm a jejich vzdálenost v=29 cm.
Vypočítejte objem a povrch koule, jestliže poloměry rovnoběžných řezů jsou r1=64 cm, r2=57 cm a jejich vzdálenost v=29 cm. - 22/7 kruh
 Vypočítejte přibližně obsah kruhu o poloměru 11 cm. Při výpočtu namísto π použijte 22/7.
Vypočítejte přibližně obsah kruhu o poloměru 11 cm. Při výpočtu namísto π použijte 22/7. - Odříznutého 72874
 V kruhu o poloměru 6 cm je struna nakreslena 3 cm od středu. Vypočítejte úhel, který svírá kord ve středu kruhu Najděte tedy délku vedlejšího oblouku odříznutého akordem.
V kruhu o poloměru 6 cm je struna nakreslena 3 cm od středu. Vypočítejte úhel, který svírá kord ve středu kruhu Najděte tedy délku vedlejšího oblouku odříznutého akordem. - Předpokládáme 4015
 Sedanka kola je ve výšce 1,2m, cyklista váží 82 kg, jede 15% kopcem dolů, rychlostí 50 km/h, narazí do obrubníku 20 cm vysokého v úhlu 45 stupňů, do jaké vzdálenosti od středu osy předního kola je cyklista vymrštěn. Předpokládáme kolo Vedora velikosti 21
Sedanka kola je ve výšce 1,2m, cyklista váží 82 kg, jede 15% kopcem dolů, rychlostí 50 km/h, narazí do obrubníku 20 cm vysokého v úhlu 45 stupňů, do jaké vzdálenosti od středu osy předního kola je cyklista vymrštěn. Předpokládáme kolo Vedora velikosti 21 - Sestrojte 4
 Sestrojte trojúhelník ABC: kružnice vepsaná má poloměr r= 2 cm, úhel alfa=50 stupňů, c= 8 cm. Proveďte náčrtek, popis konstrukce a rozbor.
Sestrojte trojúhelník ABC: kružnice vepsaná má poloměr r= 2 cm, úhel alfa=50 stupňů, c= 8 cm. Proveďte náčrtek, popis konstrukce a rozbor. - Seříznutého 61023
 Horní a dolní poloměr seříznutého pravého kruhového kužele je 8 cm a 32 cm. Je-li výška seříznutého okraje 10 cm, jak daleko od spodní základny musí být vytvořena rovina řezu, aby se vytvořily dva podobné seříznuté kužele?
Horní a dolní poloměr seříznutého pravého kruhového kužele je 8 cm a 32 cm. Je-li výška seříznutého okraje 10 cm, jak daleko od spodní základny musí být vytvořena rovina řezu, aby se vytvořily dva podobné seříznuté kužele? - Rychlík a Os vlak
 Z místa A vyjede v 7:15 rychlík rychlostí 85 km/h do B. Z B vyjede v 8:30 osobní vlak směrem do A rychlostí 55 km/h. Vzdálenost A a B je 386 1/4 km. V kolik hodin a v jaké vzdálenosti od B se oba vlaky potkají?
Z místa A vyjede v 7:15 rychlík rychlostí 85 km/h do B. Z B vyjede v 8:30 osobní vlak směrem do A rychlostí 55 km/h. Vzdálenost A a B je 386 1/4 km. V kolik hodin a v jaké vzdálenosti od B se oba vlaky potkají? - Čtvrtkruh II
 Vypočítejte poloměr čtvrtkruhu, jehož obsah se rovná kruhu o poloměru r = 46 cm.
Vypočítejte poloměr čtvrtkruhu, jehož obsah se rovná kruhu o poloměru r = 46 cm. - Vypočítej 64734
 Kouli o průměru 10dm jsme prořízli na dvě stejné části. Vypočítej plochu řezu.
Kouli o průměru 10dm jsme prořízli na dvě stejné části. Vypočítej plochu řezu. - Do odměrného
 Do odměrného válce o vnitřním průměru 10 cm jsou uloženy 4 kovové koule o průměru 5 cm. Jaké nejmenší množství vody je třeba do válce nalít, aby všecky 4 koule byly pod hladinou?
Do odměrného válce o vnitřním průměru 10 cm jsou uloženy 4 kovové koule o průměru 5 cm. Jaké nejmenší množství vody je třeba do válce nalít, aby všecky 4 koule byly pod hladinou? - Tětiva
 V kružnici o poloměru r = 70 cm je tětiva 10 × delší než její vzdálenost od středu. Jaká je délka tětivy?
V kružnici o poloměru r = 70 cm je tětiva 10 × delší než její vzdálenost od středu. Jaká je délka tětivy? - Dva kruhy
 Jsou dány dva kruhy o stejném poloměru r=1. Střed druhého kruhu leží na obvodu toho prvního. Jaká je plocha čtverce vepsaného do proniku zadaných kruhů?
Jsou dány dva kruhy o stejném poloměru r=1. Střed druhého kruhu leží na obvodu toho prvního. Jaká je plocha čtverce vepsaného do proniku zadaných kruhů? - Park
 V nově budovaném parku budou trvale umístěny otáčivé postřikovače na kropení trávníků. Urči největší poloměr kruhu, který může zavlažovat postřikovač P tak, aby nekropil návštěvníky parku na cestě AB. Vzdálenosti AB = 55 m, AP = 36 m a BP = 28 m.
V nově budovaném parku budou trvale umístěny otáčivé postřikovače na kropení trávníků. Urči největší poloměr kruhu, který může zavlažovat postřikovač P tak, aby nekropil návštěvníky parku na cestě AB. Vzdálenosti AB = 55 m, AP = 36 m a BP = 28 m.
