Vepsaná kruhu
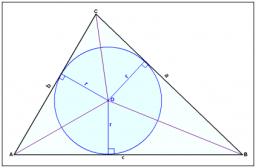
Napište rovnici kružnice vepsané trojúhelníku KLM, je-li K[ 2,1], L[6,4], M[6,1].
Správná odpověď:
Zobrazuji 5 komentářů:
Žák
Pouzity postup je pro stred teziste. Proc je to pouzito pro vypocet stredu kruznice vepsane?
Dr Math
kružnice je vepsaná trojúhelníku, pokud se dotýká všech tří stran, tedy má s každou stranou společný právě jeden bod. Střed kružnice vepsané se pak nachází v průsečíku všech os úhlů.
mate pravdu, ne v Tezisti !! , leda ze by to byt rovnostranny trojuhelnik
mate pravdu, ne v Tezisti !! , leda ze by to byt rovnostranny trojuhelnik
Dr Math
Souřadnice středu vepsané kružnice jsou vážené průměry souřadnic vrcholů, kde váhy jsou délky odpovídajících stran.
Tipy na související online kalkulačky
Hledáte statistickou kalkulačku?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Do kosočtverce
 Najděte rovnici kružnice vepsané do kosočtverce ABCD, jestliže souřadnice vrcholů jsou A [1, -2], B [8, -3] a C [9, 4].
Najděte rovnici kružnice vepsané do kosočtverce ABCD, jestliže souřadnice vrcholů jsou A [1, -2], B [8, -3] a C [9, 4]. - Výška parametrická
 Napište parametrické rovnice výšky Vc v trojúhelníku ABC: A=[5;6], B=[-2;4], C=[6;-1]
Napište parametrické rovnice výšky Vc v trojúhelníku ABC: A=[5;6], B=[-2;4], C=[6;-1] - Kružnice
 Napište rovnici kružnice která procházi bodem [0,6] a dotýka se osy x v bode [5,0]: (x-x_S)²+(y-y_S)²=r²
Napište rovnici kružnice která procházi bodem [0,6] a dotýka se osy x v bode [5,0]: (x-x_S)²+(y-y_S)²=r² - Paraboly 80525
 Napište rovnici paraboly, která prochází body: A[1,1] B[3,-1] C[1,2]
Napište rovnici paraboly, která prochází body: A[1,1] B[3,-1] C[1,2]
- Napište 3
 Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0.
Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0. - Souřadnicovými 82580
 Napište rovnici elipsy, která prochází body a její osy jsou totožné se souřadnicovými osami, když: A = [2, 3] a B = [−1, −4].
Napište rovnici elipsy, která prochází body a její osy jsou totožné se souřadnicovými osami, když: A = [2, 3] a B = [−1, −4]. - Hyperbola
 Napište rovnici hyperboly, která prochází bodem M [30; 24] a má ohniska v bodech F1 [0;4odmocniny ze 6], F2 [0; -4odmocniny ze 6].
Napište rovnici hyperboly, která prochází bodem M [30; 24] a má ohniska v bodech F1 [0;4odmocniny ze 6], F2 [0; -4odmocniny ze 6]. - Trojúhelník 2604
 Daný je trojúhelník ABC: A[-3;-1] B[5;3] C[1;5] Napište rovnici přímky, která prohází vrcholem C rovnoběžně se stranou AB.
Daný je trojúhelník ABC: A[-3;-1] B[5;3] C[1;5] Napište rovnici přímky, která prohází vrcholem C rovnoběžně se stranou AB. - 9x^2−4y^2=36 82642
 Napište rovnici tečny hyperboly 9x²−4y²=36 v bodě T =[t1,4].
Napište rovnici tečny hyperboly 9x²−4y²=36 v bodě T =[t1,4].
- Trojúhelník KLM
 Je dán trojúhelník KLM body K[-3,2] L[7,-3] M[8,5] Vypočtěte délky stran a obvod.
Je dán trojúhelník KLM body K[-3,2] L[7,-3] M[8,5] Vypočtěte délky stran a obvod. - Vrcholy trojúhelníku
 Určete souřadnice vrcholu trojúhelníku ABC, známe-li středy SAB [0;3] SBC [1;6] SAC [4;5], jeho stran AB, BC, AC.
Určete souřadnice vrcholu trojúhelníku ABC, známe-li středy SAB [0;3] SBC [1;6] SAC [4;5], jeho stran AB, BC, AC. - Vypočítejte 198
 Vypočítejte obsah a obvod pravoúhlého trojúhelníku ABC, je-li A[5,5;-2,5] B[-3;5] C[-3;-2,5]
Vypočítejte obsah a obvod pravoúhlého trojúhelníku ABC, je-li A[5,5;-2,5] B[-3;5] C[-3;-2,5] - Vzdálenost 82341
 Určete rovnici kružnice, která je množinou všech bodů roviny, které mají od bodu [3,7] dvakrát větší vzdálenost než od bodu [0,1].
Určete rovnici kružnice, která je množinou všech bodů roviny, které mají od bodu [3,7] dvakrát větší vzdálenost než od bodu [0,1]. - Obecná rovnice
 Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná
Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná
- Trojúhelník 55311
 Sestrojte trojúhelník KLM kde strana k má 6,7cm; těžnice na stranu k je 4,1cm a úhel LKM má 63 stupňů. Napište postup konstrukce.
Sestrojte trojúhelník KLM kde strana k má 6,7cm; těžnice na stranu k je 4,1cm a úhel LKM má 63 stupňů. Napište postup konstrukce. - Těžiště
 V trojúhelníku ABC leží bod D[1,-2,6], který je středem strany |BC| a bod G, který je těžištěm trojúhelníku G[8,1,-3]. Najděte souřadnice vrcholu A[x,y,z].
V trojúhelníku ABC leží bod D[1,-2,6], který je středem strany |BC| a bod G, který je těžištěm trojúhelníku G[8,1,-3]. Najděte souřadnice vrcholu A[x,y,z]. - Smernicový tvar
 Najděte rovnici přímky procházející bodem X [8, 1] a sklonem - směrnicí -2,8. Odpověď zapište ve tvaru y = ax + b, kde a, b jsou konstanty.
Najděte rovnici přímky procházející bodem X [8, 1] a sklonem - směrnicí -2,8. Odpověď zapište ve tvaru y = ax + b, kde a, b jsou konstanty.
