Lichoběžník - čtyri strany
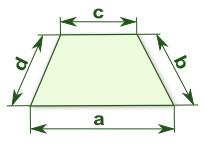
lichoběžník- 40,5+42,5+52,8+35,0. Vypočti obsah
Správná odpověď:
Zobrazuji 5 komentářů:
Mo - Ofic
jsem chtel jen upozornit ze je dulezite vedet ktere strany lichobezniku jsou rovnobezne; jinak obecny 4-uhelnik se da vypocitet jen ze souradnic (tak cini i geodety), ne z delek stran.
Žák
Musím přiznat, že k tomuto úkolu jsem došla proto, že můj vnuk propadá z matiky. Nikdy v životě jsem neslyšela o " HERONOVĚ VZORCI ", který je třeba znát, aby se tento příklad vypočítal. Vypočítá se obsah trojúhelníku na základě známých velikostí stran a z toho potom výška trojúhelníku. Tato výška je výškou lichoběžníku. Když budeš vědět co hledáš, tak návod najdeš !
Žák
Vypočítá se obsah trojúhelníku na základě známých velikostí stran => to sa vola heronov vzorec. Teda nevim co reklamujes, ze obsah ze tri stran se pocita podle Heronovho vzorce?
Existuju zjednusene vzorce pre napr. pravouhly nebo rovnostranny trojuhelnik....
Existuju zjednusene vzorce pre napr. pravouhly nebo rovnostranny trojuhelnik....
Dr Math
obsah lichoběžníku pomocí 4 stran - v podstate trojuhelnik SSS tam zvnikne pokud rozdelime lichobeznik na obdelnik a dva pravouhle trojuhelniky. Tie dva trojuhelniky maji strany b,d, a (a-c)
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Převod
 Vypočti a převeď: 0,2m² + 80dm² + 200cm² = kolik m2
Vypočti a převeď: 0,2m² + 80dm² + 200cm² = kolik m2 - Vypočti výrazy
 Vypočti: a/2 + 3*4 - 5*4 + 3 b/2 + 3*(4 - 5)*(4 + 3) c/2 + [3*4 - (5*4 + 3)] d/{2 + [3*(4 - 5)]*4} + 3 e/2 + {3* [4 - 5*(4 + 3)]}
Vypočti: a/2 + 3*4 - 5*4 + 3 b/2 + 3*(4 - 5)*(4 + 3) c/2 + [3*4 - (5*4 + 3)] d/{2 + [3*(4 - 5)]*4} + 3 e/2 + {3* [4 - 5*(4 + 3)]} - Lichoběžník
 Délky rovnoběžných stran lichoběžníku jsou (2x + 3) a (x + 8) a vzdálenost mezi nimi je (x + 4). Pokud je plocha lichoběžníku je 590, najděte hodnotu x.
Délky rovnoběžných stran lichoběžníku jsou (2x + 3) a (x + 8) a vzdálenost mezi nimi je (x + 4). Pokud je plocha lichoběžníku je 590, najděte hodnotu x. - Lichoběžník
 Plocha lichoběžníku je 266. Co je hodnota x je-li základny: b1 je 2x-3, b2 je 2x + 1 a výška h je x + 4
Plocha lichoběžníku je 266. Co je hodnota x je-li základny: b1 je 2x-3, b2 je 2x + 1 a výška h je x + 4 - Řez železničním
 Řez železničním náspem je rovnoramenný lichoběžník, jehož velikosti základen jsou v poměru 5:3. Ramena mají délku 5 m a výška násypu je 4,8m. Vypočti velikost plochy řezu náspu.
Řez železničním náspem je rovnoramenný lichoběžník, jehož velikosti základen jsou v poměru 5:3. Ramena mají délku 5 m a výška násypu je 4,8m. Vypočti velikost plochy řezu náspu. - Lichoběžník 5341
 Lichoběžník, kde AB je rovnoběžná s CD, má úhel A : úhel D = 4 : 5, úhel B = 3x-15 a úhel C = 4x+20. Najděte úhel A, B, C a D.
Lichoběžník, kde AB je rovnoběžná s CD, má úhel A : úhel D = 4 : 5, úhel B = 3x-15 a úhel C = 4x+20. Najděte úhel A, B, C a D. - Paralelně R+3R
 Do obvodu jsme paralelně zapojili dva rezistory, přičemž první má třikrát větší odpor než druhý. Napětí mezi svorkami každého rezistoru je 6 V. Vypočti, jaký proud prochází každou větví, když výsledný odpor obou rezistorů je 15 ohmů.
Do obvodu jsme paralelně zapojili dva rezistory, přičemž první má třikrát větší odpor než druhý. Napětí mezi svorkami každého rezistoru je 6 V. Vypočti, jaký proud prochází každou větví, když výsledný odpor obou rezistorů je 15 ohmů. - Lichoběžníku 7862
 Velikost lichoběžníku je 3/4*x cm, x cm, 2*(x+1) cm a 3(x+2) cm. Pokud je jeho obvod 60 cm, vypočítejte délku každé strany.
Velikost lichoběžníku je 3/4*x cm, x cm, 2*(x+1) cm a 3(x+2) cm. Pokud je jeho obvod 60 cm, vypočítejte délku každé strany. - Lichoběžník 7052
 Je dán lichoběžník ABCD (AB||CD, AB kolmé na AD). Vypočti jeho obvod, pokud |AB|=20cm, |CD|=15cm, |AD|=12cm. Pythagorova věta
Je dán lichoběžník ABCD (AB||CD, AB kolmé na AD). Vypočti jeho obvod, pokud |AB|=20cm, |CD|=15cm, |AD|=12cm. Pythagorova věta - Profil
 Profil příkopu je rovnoramenný lichoběžník se základnami o délce 80m a 60m. Sklon boční stěny příkopu je 80°. Výpočti hloubku příkopu.
Profil příkopu je rovnoramenný lichoběžník se základnami o délce 80m a 60m. Sklon boční stěny příkopu je 80°. Výpočti hloubku příkopu. - Lichoběžníku 80955
 Obvod lichoběžníku = 39a-7. Tři strany mají následující délku: 9a, 5a+1 a 17a-6. Jaká je délka čtvrté strany?
Obvod lichoběžníku = 39a-7. Tři strany mají následující délku: 9a, 5a+1 a 17a-6. Jaká je délka čtvrté strany? - Plavecký
 Plavecký bazén dlouhý 30 metrů je naplněn vodou do hloubky 1 metru na mělkém konci a 5 metrů na hlubokém konci a svislé ploše bazénu má tvar lichoběžníku s plochou danou S (abcd). = 1/2 (ab + cd) x ad. Jaká je plocha průřezu abcd?
Plavecký bazén dlouhý 30 metrů je naplněn vodou do hloubky 1 metru na mělkém konci a 5 metrů na hlubokém konci a svislé ploše bazénu má tvar lichoběžníku s plochou danou S (abcd). = 1/2 (ab + cd) x ad. Jaká je plocha průřezu abcd? - Šetiůhelník
 Vypočti obsah pravidelného šetiůhelníku o straně a=2cm
Vypočti obsah pravidelného šetiůhelníku o straně a=2cm - Dvanáctiúhelník
 Vypočti obsah pravidelného dvanáctiúhelníku jestliže poloměr kružnice opsané je 5 cm.
Vypočti obsah pravidelného dvanáctiúhelníku jestliže poloměr kružnice opsané je 5 cm. - Ze vzorce
 Ze vzorce povrchu kvádru S=2. (ab+ac+bc) vyjádři neznámou c. C =?
Ze vzorce povrchu kvádru S=2. (ab+ac+bc) vyjádři neznámou c. C =? - Lichoběžníku 44431
 1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky
1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky - XY trojúhelník
 Vypočítejte obsah trojúhelníku, který tvoří přímka 7x+8y-69=0 se souřadnicovými osami.
Vypočítejte obsah trojúhelníku, který tvoří přímka 7x+8y-69=0 se souřadnicovými osami.
