Stan
Stan tvaru pravidelného čtyřbokého jehlanu má délku podstavné hrany a=2m a výšku v=1,8m. Kolik m2 plátna potřebujeme na ušití stanu, musíme-li přidat 7% na švy? Kolik m3 bude ve stanu?
Správná odpověď:

Tipy na související online kalkulačky
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- stereometrie
- jehlan
- povrch tělesa
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- základní funkce
- procenta
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Přístřešek
 Přístřešek má tvar pravidelného čtyřbokého jehlanu bez přední stěny. Délka podstavné hrany je 3 metry, výška přístřešku je 3,5metru. Kolik plátna je potřeba koupit na jeho ušití, jestliže musíme navýšit spotřebu o 20% na přehyby a prostřihy.
Přístřešek má tvar pravidelného čtyřbokého jehlanu bez přední stěny. Délka podstavné hrany je 3 metry, výška přístřešku je 3,5metru. Kolik plátna je potřeba koupit na jeho ušití, jestliže musíme navýšit spotřebu o 20% na přehyby a prostřihy. - Pravidelného 19133
 Dětský stan s podlahou z bukového dřeva má tvar pravidelného čtyřbokého jehlanu s hranou podstavy 1,25 m a výškou 80cm. Kolik m² celtoviny potřebujeme dokončení stanu, pokud na záhyby potřebujeme přidat 12% materiálu?
Dětský stan s podlahou z bukového dřeva má tvar pravidelného čtyřbokého jehlanu s hranou podstavy 1,25 m a výškou 80cm. Kolik m² celtoviny potřebujeme dokončení stanu, pokud na záhyby potřebujeme přidat 12% materiálu? - Stan s
 Stan s podlážkou má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou a= 2,4 m, výškou= 1,8 m. Kolik plátna je potřeba na stan?
Stan s podlážkou má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou a= 2,4 m, výškou= 1,8 m. Kolik plátna je potřeba na stan? - Stan má
 Stan má tvar pláště pravidelného čtyřbokého jehlanu o podstavné hraně a=3,5metru a výšce 2,4metru. Kolik krychlových metrů vzduchu obsahuje?
Stan má tvar pláště pravidelného čtyřbokého jehlanu o podstavné hraně a=3,5metru a výšce 2,4metru. Kolik krychlových metrů vzduchu obsahuje?
- Vypočítej 50
 Vypočítej objem pravidelného čtyřbokého jehlanu, který má velikost podstavné hrany a = 12 cm a výšku 11 cm.
Vypočítej objem pravidelného čtyřbokého jehlanu, který má velikost podstavné hrany a = 12 cm a výšku 11 cm. - Plocha stanu
 Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m.
Vypočítejte, kolik plátna (bez podlahy) se spotřebuje na zhotovení stanu, který má tvar pravidelného čtyřbokého jehlanu. Hrana podstavy má délku 3 m a výška stanu je 2m. - Počítáme-li 7820
 Stan tvaru jehlanu má podstavu čtverce o velikosti strany 2,2m a výšku 1,8m. Kolik metrů čtverečních stanového plátna je třeba na jeho zhotovení počítáme-li pět procent navíc na založení?
Stan tvaru jehlanu má podstavu čtverce o velikosti strany 2,2m a výšku 1,8m. Kolik metrů čtverečních stanového plátna je třeba na jeho zhotovení počítáme-li pět procent navíc na založení? - Tajný poklad
 Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad.
Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad. - Věž
 Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%.
Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%.
- Zmrzlinář
 Zmrzlinář Eda vymyslel nový hezký kornout tvaru pravidelného čtyřbokého jehlanu, v němž bude prodávat svoji zmrzlinu. Kornout bude mít délku boční hrany 5cm a stěnovou výšku 4cm. Aby mu ji mohli v továrně sériově vyrábět, potřebují ještě určit rozměry pod
Zmrzlinář Eda vymyslel nový hezký kornout tvaru pravidelného čtyřbokého jehlanu, v němž bude prodávat svoji zmrzlinu. Kornout bude mít délku boční hrany 5cm a stěnovou výšku 4cm. Aby mu ji mohli v továrně sériově vyrábět, potřebují ještě určit rozměry pod - Stan pro skauty
 Stan pro skauty má dřevěnou obdélníkovou podsadu s rozměry 220 cm a 150 cm. Kolik plátna je třeba na střechu tvaru čtyřbokého jehlanu vysokého 170 cm?
Stan pro skauty má dřevěnou obdélníkovou podsadu s rozměry 220 cm a 150 cm. Kolik plátna je třeba na střechu tvaru čtyřbokého jehlanu vysokého 170 cm? - Stan
 Stan tvaru jehlanu má podstavu čtverec s délkou strany 2 m a výškou 1,7 m. Kolik m² plátna třeba na jeho provedení, když na odpad je třeba připočítat ještě 10%?
Stan tvaru jehlanu má podstavu čtverec s délkou strany 2 m a výškou 1,7 m. Kolik m² plátna třeba na jeho provedení, když na odpad je třeba připočítat ještě 10%? - Pravidelného 83324
 Objem pravidelného čtyřbokého jehlanu je 72 cm³. Jeho výška se rovná délce podstavné hrany. Vypočítej délku podstavné a povrch jehlanu.
Objem pravidelného čtyřbokého jehlanu je 72 cm³. Jeho výška se rovná délce podstavné hrany. Vypočítej délku podstavné a povrch jehlanu. - Vypočítej 40
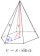 Vypočítej objem pravidelného čtyřbokého jehlanu, který má velikost podstavné hrany a = 8 cm a velikost boční hrany h = 9 cm.
Vypočítej objem pravidelného čtyřbokého jehlanu, který má velikost podstavné hrany a = 8 cm a velikost boční hrany h = 9 cm.
- Pravidelný 11
 Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu
Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu - Pravidelného 6138
 Jaká je výška stanu tvaru pravidelného čtyřbokého jehlanu, jehož objem je 3 dm³ a podstava má obsah 6 dm²?
Jaká je výška stanu tvaru pravidelného čtyřbokého jehlanu, jehož objem je 3 dm³ a podstava má obsah 6 dm²? - Střecha 14
 Střecha rekreační montované chaty má tvar pravidelného čtyřbokého jehlanu s délkou podstavné hrany 8 metrů a výškou 9 m. Kolik čtverečných metrů lepenky je třeba k pokrytí střechy?
Střecha rekreační montované chaty má tvar pravidelného čtyřbokého jehlanu s délkou podstavné hrany 8 metrů a výškou 9 m. Kolik čtverečných metrů lepenky je třeba k pokrytí střechy?
