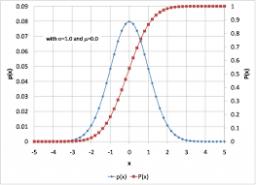
Distribuční funkce
X 2 3 4
p 0,3 0,35 0,35
Pro údaje v této tabulce mám vypočítat distribuční funkci F (x) a dále p (2,5 < ξ < 3,25), p (2,8 < ξ) a p (3,25 > ξ)
p 0,3 0,35 0,35
Pro údaje v této tabulce mám vypočítat distribuční funkci F (x) a dále p (2,5 < ξ < 3,25), p (2,8 < ξ) a p (3,25 > ξ)
Správná odpověď:
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Střelec 5
 Střelec má tři náboje. Rozhodl se, že bude střílet na terč, dokud se poprvé netrefí. Pravděpodobnost zásahu je při každém výstřelu 0,6. Náhodná veličina X udává počet vystřelených nábojů. a) Napište rozdělení pravděpodobností náhodné veličiny X a její dis
Střelec má tři náboje. Rozhodl se, že bude střílet na terč, dokud se poprvé netrefí. Pravděpodobnost zásahu je při každém výstřelu 0,6. Náhodná veličina X udává počet vystřelených nábojů. a) Napište rozdělení pravděpodobností náhodné veličiny X a její dis - Statistický 6399
 Pro statistický soubor: 2,3; 3,4; 1,8; 3,2; 3,2; 1,9; 3,3; 4,5; 4,3; 5,0; 4,8; 4,3; 4,3; 1,9 určete výběrový rozptyl a medián, az empirické distribuční funkce určete P(2,1 < ξ < 3,5).
Pro statistický soubor: 2,3; 3,4; 1,8; 3,2; 3,2; 1,9; 3,3; 4,5; 4,3; 5,0; 4,8; 4,3; 4,3; 1,9 určete výběrový rozptyl a medián, az empirické distribuční funkce určete P(2,1 < ξ < 3,5). - Pravděpodobností 29371
 Nechť náhodná veličina ξ představuje počet spokojených zákazníků. Pravděpodobnost spokojeného zákazníka u každého ze čtyř zákazníků je 7/10. Určete: a) rozdělení pravděpodobností, distribuční funkci F(x) a P(-0,5 < ξ < 3,1) b) rozptyl náhodné veliči
Nechť náhodná veličina ξ představuje počet spokojených zákazníků. Pravděpodobnost spokojeného zákazníka u každého ze čtyř zákazníků je 7/10. Určete: a) rozdělení pravděpodobností, distribuční funkci F(x) a P(-0,5 < ξ < 3,1) b) rozptyl náhodné veliči - Telefónne hovory
 Náhodná veličina, která modeluje dobu mezi 2 telef. Hovory má exponenciální rozdělení s hustotou f(x)=10exp (-10x), x je větší než 0. Spočítej její distribuční funkci a pravděpodobnost, že doba mezi hovory nepřekročí 5 sekund, doba mezi hovory překročí 15
Náhodná veličina, která modeluje dobu mezi 2 telef. Hovory má exponenciální rozdělení s hustotou f(x)=10exp (-10x), x je větší než 0. Spočítej její distribuční funkci a pravděpodobnost, že doba mezi hovory nepřekročí 5 sekund, doba mezi hovory překročí 15 - Pravděpodobností 44941
 Ve volbách stranu Z volilo 2400000 voličů z celkového počtu 6000000 voličů. Vyberme náhodně tři voliče a uvažujme náhodnou veličinu ξ={počet voličů strany Z ve výběru ze tří voličů}. Určete a) rozdělení pravděpodobností, distribuční funkci F(x) a P(0,8< ξ
Ve volbách stranu Z volilo 2400000 voličů z celkového počtu 6000000 voličů. Vyberme náhodně tři voliče a uvažujme náhodnou veličinu ξ={počet voličů strany Z ve výběru ze tří voličů}. Určete a) rozdělení pravděpodobností, distribuční funkci F(x) a P(0,8< ξ - Pravděpodobností 45201
 Ve volbách stranu Z volilo 2400000 voličů z celkového počtu 6000000 voličů. Vyberme náhodně tři voliče a uvažujme náhodnou veličinu ξ={počet voličů strany Z ve výběru ze tří voličů}. Určete a) rozdělení pravděpodobností, distribuční funkci F(x) a P(0,8< ξ
Ve volbách stranu Z volilo 2400000 voličů z celkového počtu 6000000 voličů. Vyberme náhodně tři voliče a uvažujme náhodnou veličinu ξ={počet voličů strany Z ve výběru ze tří voličů}. Určete a) rozdělení pravděpodobností, distribuční funkci F(x) a P(0,8< ξ - Rovnice 39
 Rovnice linearní funkcí je : y=-3x+4 a) urči průsečíky s osami načrtni graf b) pro které x platí f(x)=-1 c) pro které x platí f(x)=0 d) pro které y platí f(-1/2)=y
Rovnice linearní funkcí je : y=-3x+4 a) urči průsečíky s osami načrtni graf b) pro které x platí f(x)=-1 c) pro které x platí f(x)=0 d) pro které y platí f(-1/2)=y - Kosmetika 8430
 V tabulce jsou uvedeny údaje, které rodina minula loni na vánoční dárky. Letos plánují snížit výdaje o 20% oproti loňskému roku. Kolik eur ušetří rodina na dárcích oproti loňskému roku? Knihy 50,50 Kosmetika 35,00 Hračky 25,50 Oblečení 39,00
V tabulce jsou uvedeny údaje, které rodina minula loni na vánoční dárky. Letos plánují snížit výdaje o 20% oproti loňskému roku. Kolik eur ušetří rodina na dárcích oproti loňskému roku? Knihy 50,50 Kosmetika 35,00 Hračky 25,50 Oblečení 39,00 - V kanceláři
 V kanceláři bude připojeno: počítač-800W, varná konvice-2,5KW, osvětlení-650W, trouba-1,9KW; elektrický sporák-3,3KW; klimatizace-6100W. Jak nejmenší průřez kabelů musíme přivést v této místnosti. Propočítat pro Měď a Hliník.
V kanceláři bude připojeno: počítač-800W, varná konvice-2,5KW, osvětlení-650W, trouba-1,9KW; elektrický sporák-3,3KW; klimatizace-6100W. Jak nejmenší průřez kabelů musíme přivést v této místnosti. Propočítat pro Měď a Hliník. - Směrodatná odchýlka
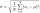 Najdete směrodatnú (standardní) odchylku pro množinu dat (seskupené údaje): Věk (roky) Počet osob 0-10 15 10-20 15 20-30 23 30-40 22 40-50 25 50-60 10 60-70 5 70-80 10
Najdete směrodatnú (standardní) odchylku pro množinu dat (seskupené údaje): Věk (roky) Počet osob 0-10 15 10-20 15 20-30 23 30-40 22 40-50 25 50-60 10 60-70 5 70-80 10 - Drahé kovy
 V letech 2006-2009 se hodnota drahých kovů rychle změnila. Údaje v následující tabulce představují celkovou míru návratnosti (v procentech) platiny, zlata, stříbra od roku 2006 do roku 2009: Rok Platinum Gold Silver 2009 62,7 25,0 56,8 2008 -41,3 4,3 -26,
V letech 2006-2009 se hodnota drahých kovů rychle změnila. Údaje v následující tabulce představují celkovou míru návratnosti (v procentech) platiny, zlata, stříbra od roku 2006 do roku 2009: Rok Platinum Gold Silver 2009 62,7 25,0 56,8 2008 -41,3 4,3 -26, - Distribuční 4907
 Je zadána spojitá náhodná velicina X: distribuční funkcí, určete parametry a; b tak, aby funkce F (x) byla spojitá a byla distribuční funkcí náhodné veličiny X a vyjádřete f (x). P (X < 5) F(x) = 0; x < 3 F(x) = a . x - b; 3 < x < 6 F(x) = 1;
Je zadána spojitá náhodná velicina X: distribuční funkcí, určete parametry a; b tak, aby funkce F (x) byla spojitá a byla distribuční funkcí náhodné veličiny X a vyjádřete f (x). P (X < 5) F(x) = 0; x < 3 F(x) = a . x - b; 3 < x < 6 F(x) = 1; - Desetinném 82325
 Čísla uvedená v tabulce hodnot míst zapište v desetinném tvaru. Stovky desítek. Jedničky. Desítky. 6. 1. 5. 4 8. 3. 2. 5 7. 9. 0. 3 1. 0. 3. 1 4. 8. 0. 7
Čísla uvedená v tabulce hodnot míst zapište v desetinném tvaru. Stovky desítek. Jedničky. Desítky. 6. 1. 5. 4 8. 3. 2. 5 7. 9. 0. 3 1. 0. 3. 1 4. 8. 0. 7 - Histogramový 1882
 Sestrojte histogramový a svíčkový graf pro dané údaje. 56, 32, 54, 32, 23, 67, 23, 45, 12, 32, 34, 24, 36, 47, 19, 43
Sestrojte histogramový a svíčkový graf pro dané údaje. 56, 32, 54, 32, 23, 67, 23, 45, 12, 32, 34, 24, 36, 47, 19, 43 - O kolik
 O kolik a kolikrát je větší 72,1 jako 0,00721?
O kolik a kolikrát je větší 72,1 jako 0,00721? - Zaokrouhlete 13451
 V tabulce níže jsou uvedeny ceny akcií, zisk na akcii a dividendy na akcii pro tři společnosti za poslední rok: Deere & Co. Cena 65,70 USD zisk na akcii 4,40 USD Dividendy na akcii 1,16 USD Cena Google 528,33 USD zisk na akcii 27,72 USD Dividendy na akcii
V tabulce níže jsou uvedeny ceny akcií, zisk na akcii a dividendy na akcii pro tři společnosti za poslední rok: Deere & Co. Cena 65,70 USD zisk na akcii 4,40 USD Dividendy na akcii 1,16 USD Cena Google 528,33 USD zisk na akcii 27,72 USD Dividendy na akcii - Směrodatnou 32751
 Tabulka je uvedena: dní stížnosti 0-4 2 5-9 4 10-14 8 15-19 6 20-24 4 25-29 3 30-34 3 1,1 Jaké procento stížností bylo vyřešeno do 2 týdnů? 1,2 vypočítat průměrný počet dní na vyřešení těchto stížností. 1,3 vypočítat modální počet dní pro vyřešení těchto
Tabulka je uvedena: dní stížnosti 0-4 2 5-9 4 10-14 8 15-19 6 20-24 4 25-29 3 30-34 3 1,1 Jaké procento stížností bylo vyřešeno do 2 týdnů? 1,2 vypočítat průměrný počet dní na vyřešení těchto stížností. 1,3 vypočítat modální počet dní pro vyřešení těchto
