Kvadratická rovnice
Řešte kvadratickou rovnici:
2x2-76x+722=0
2x2-76x+722=0
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Kvadr. rovnica
 Rešte kvadratickou rovnici: 2x²- 2(x-7)²+5x=0
Rešte kvadratickou rovnici: 2x²- 2(x-7)²+5x=0 - Rýze kvadratická rovnice
 Řešte ryze kvadratickou rovnici -5x² +7 = 0.
Řešte ryze kvadratickou rovnici -5x² +7 = 0. - Vyřeš
 Vyřeš kvadratickou rovnici: 2y²-8y+12=0
Vyřeš kvadratickou rovnici: 2y²-8y+12=0 - Rovnici: 5482
 Řešte rovnici: 0,5 • (3+ x) -0,2 • (0,5x-5) = 0
Řešte rovnici: 0,5 • (3+ x) -0,2 • (0,5x-5) = 0 - Rovnice v podílovém tvaru
 Rešte rovnici v podílovém tvaru: 6x*(3x-2)/x+7=0
Rešte rovnici v podílovém tvaru: 6x*(3x-2)/x+7=0 - Rovnici: 6200
 Řešte rovnici: 2y=4(0,5+3/2)-1
Řešte rovnici: 2y=4(0,5+3/2)-1 - Rovnice 19
 Řešte rovnici s iks (x): 3(1/3+2x)-2(1/3-3x)-13/2=0
Řešte rovnici s iks (x): 3(1/3+2x)-2(1/3-3x)-13/2=0 - Variace - druhé třídy - II
 řešte rovnici: V(2, x+8)=72
řešte rovnici: V(2, x+8)=72 - Rovnice 27
 Řešte rovnici: (2v+2)/8=(v-7)/4-v
Řešte rovnici: (2v+2)/8=(v-7)/4-v - Rovnička
 Řešte rovnici: 3x-2(x-1)=1,5x+0,5(4-2x)
Řešte rovnici: 3x-2(x-1)=1,5x+0,5(4-2x) - Rovnice 29
 Řešte následujíci rovnici: 2 ( 2x + 3 ) = 8 ( 1 - x) -5 ( x -2 )
Řešte následujíci rovnici: 2 ( 2x + 3 ) = 8 ( 1 - x) -5 ( x -2 ) - Kvadratickou 33371
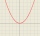 Řešte kvadratickou nerovnici: -2x² + 4x + 6 < 0
Řešte kvadratickou nerovnici: -2x² + 4x + 6 < 0 - Lineárni rovnica se zlomkama
 Řešte v R následující lineární rovnici: 4/10X+2/10X+1/6X+1/10X+400=X
Řešte v R následující lineární rovnici: 4/10X+2/10X+1/6X+1/10X+400=X - Rovnice 24
 Řešte rovnici se zlomky: x/3-x/8=x/12+x/8
Řešte rovnici se zlomky: x/3-x/8=x/12+x/8 - Rovnice
 Řešte rovnici a provedte zkoušku: 1-(x-x/7-1/7)= 7-9x/2 +5/2
Řešte rovnici a provedte zkoušku: 1-(x-x/7-1/7)= 7-9x/2 +5/2 - Rovnice
 Řešte rovnici a proveďte zkoušku: 2(4x + 3) - 2 = 6 - 5(1 - x)
Řešte rovnici a proveďte zkoušku: 2(4x + 3) - 2 = 6 - 5(1 - x) - Rovnice jednoduchá
 Řešte následující jednoduchou rovnici: 2. (4x + 3) = 2-5. (1-x)
Řešte následující jednoduchou rovnici: 2. (4x + 3) = 2-5. (1-x)
