MO-I-Z6
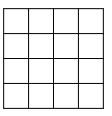
Čtverec se stranou 4 cm je rozdělen na čtverečky se stranou 1 cm jako na obrázku.
Rozdělte čtverec podél vyznačených čar na dva útvary s obvodem 16 cm. Najděte alespoň tři různá řešení (tzn. taková tři řešení, aby žádný útvar jednoho řešení nebyl shodný s žádným útvarem jiného řešení).
Rozdělte čtverec podél vyznačených čar na dva útvary s obvodem 16 cm. Najděte alespoň tři různá řešení (tzn. taková tři řešení, aby žádný útvar jednoho řešení nebyl shodný s žádným útvarem jiného řešení).
Správná odpověď:
Zobrazuji 2 komentáře:
Žák
jedno řešení su dva útvary:
####
#
##
a druhy s obvodem je doplněk do čtverce, také mě obvod 16.
Stačí se s tim pohrát - útvary musí mít přibližně stejný obsah aby měly stejný obvod.
####
#
##
a druhy s obvodem je doplněk do čtverce, také mě obvod 16.
Stačí se s tim pohrát - útvary musí mít přibližně stejný obsah aby měly stejný obvod.
7 let 4 Likes
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Trojúhelník 64614
 Seřaďte dané útvary podle jejich plošného obsahu, sestupně: čtverec s obvodem = 16 cm; Obdélník se stranou a = 3 cm a obvodem o = 16 cm; Pravoúhlý trojúhelník s odvěsnou dlouhou 4,125 cm a přeponou 8,125 cm.
Seřaďte dané útvary podle jejich plošného obsahu, sestupně: čtverec s obvodem = 16 cm; Obdélník se stranou a = 3 cm a obvodem o = 16 cm; Pravoúhlý trojúhelník s odvěsnou dlouhou 4,125 cm a přeponou 8,125 cm. - Čtvercova sít
 Čtvercova síť se skladá ze čtverců se stranou delky 1cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6cm² a obvod 12cm a aby jejich strany splývaly s přímkami síťe.
Čtvercova síť se skladá ze čtverců se stranou delky 1cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6cm² a obvod 12cm a aby jejich strany splývaly s přímkami síťe. - Tři obdélníky
 Rozdělte čtverec se stranou délky 12 cm na tři obdélníky se stejnými obvody tak, aby tyto obvody byly co nejmenší.
Rozdělte čtverec se stranou délky 12 cm na tři obdélníky se stejnými obvody tak, aby tyto obvody byly co nejmenší. - Čtverec nebo obdélníky
 Rozhodni, které útvary mají větší obsah: a) čtverec se stranou 8cm nebo b) dva obdélníku se stranami 5cm a 15cm? Zapiš výsledek jako 1 nebo 2 (obdélníky)
Rozhodni, které útvary mají větší obsah: a) čtverec se stranou 8cm nebo b) dva obdélníku se stranami 5cm a 15cm? Zapiš výsledek jako 1 nebo 2 (obdélníky) - Nerozlišují 37083
 Na hřišti jsou nakresleny tři stejně velké kruhy. Rozestavte 16 kuželek tak, aby v každém kruhu stálo 9 kuželek. Najděte alespoň osm podstatně odlišných rozestavení, tzn. J. takových rozestavení, při kterých se nerozlišují kuželky ani kruhy.
Na hřišti jsou nakresleny tři stejně velké kruhy. Rozestavte 16 kuželek tak, aby v každém kruhu stálo 9 kuželek. Najděte alespoň osm podstatně odlišných rozestavení, tzn. J. takových rozestavení, při kterých se nerozlišují kuželky ani kruhy. - Obdélníkové 8136
 Rozdělte čtvercovou zahradu s obvodem 124 m na dvě obdélníkové zahrady tak, aby plot jedné zahrady byl o 10 m delší než plot druhé zahrady. Jaké rozměry budou mít tyto obdélníkové zahrady?
Rozdělte čtvercovou zahradu s obvodem 124 m na dvě obdélníkové zahrady tak, aby plot jedné zahrady byl o 10 m delší než plot druhé zahrady. Jaké rozměry budou mít tyto obdélníkové zahrady? - Kříž 5
 Útvar na obrázku je složen ze stejných čtverců a má obsah 45cm². Jaký je jeho obvod?
Útvar na obrázku je složen ze stejných čtverců a má obsah 45cm². Jaký je jeho obvod? - Geometrická posloupnost
 Mezi čísla 4 a -4000 vložte 2 čísla, aby tvořily geometrickou posloupnost.
Mezi čísla 4 a -4000 vložte 2 čísla, aby tvořily geometrickou posloupnost. - Obdélníky 8142
 Rozdělte obdélník se stranami dlouhými 60 mm a 84 mm na tři obdélníky se stejným obvodem.
Rozdělte obdélník se stranami dlouhými 60 mm a 84 mm na tři obdélníky se stejným obvodem. - Čtyřúhelníku 66614
 Na obrázku je čtverec ABCD se středem S a stranou dlouhou 8 cm. Bod E je libovolný bod strany CD různé od C a D. Vypočítejte obsah čtyřúhelníku ASBE v cm².
Na obrázku je čtverec ABCD se středem S a stranou dlouhou 8 cm. Bod E je libovolný bod strany CD různé od C a D. Vypočítejte obsah čtyřúhelníku ASBE v cm². - Klempíř
 Klempíř měl rozstříhat pás plechu o rozměrech 380 cm a 60cm na co největší čtverec tak, aby nevznikl žádný odpad. Vypočítej délku strany jednoho čtverce. Kolik čtverců nastříhal?
Klempíř měl rozstříhat pás plechu o rozměrech 380 cm a 60cm na co největší čtverec tak, aby nevznikl žádný odpad. Vypočítej délku strany jednoho čtverce. Kolik čtverců nastříhal? - Zlatý řez
 Rozdělte úsečku délky 153 cm na dva úseky tak, aby poměr menšího dílu ke většímu byl stejný jako poměr většího dílu k délce celé úsečky.
Rozdělte úsečku délky 153 cm na dva úseky tak, aby poměr menšího dílu ke většímu byl stejný jako poměr většího dílu k délce celé úsečky. - Kvádr na krychlu
 Kvádr s rozměry 9 cm, 6 cm a 4 cm má shodný objem jako krychle. Vypočtěte povrch této krychle.
Kvádr s rozměry 9 cm, 6 cm a 4 cm má shodný objem jako krychle. Vypočtěte povrch této krychle. - Moivrovka
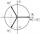 Existují dvě různá komplexní čísla z taková, že z na třetí se rovná 1 a současně z není rovno 1. Vypočtěte součet těchto dvou čísel.
Existují dvě různá komplexní čísla z taková, že z na třetí se rovná 1 a současně z není rovno 1. Vypočtěte součet těchto dvou čísel. - Myška Hryzka
 Myška Hryzka našla 27 stejných krychliček sýra. Nejdříve si z nich poskládala velkou krychli a chvíli počkala, než se sýrové krychličky k sobě přilepily. Potom z každé stěny velké krychle vyhryzla střední krychličku. Poté snědla i krychličku, která byla v
Myška Hryzka našla 27 stejných krychliček sýra. Nejdříve si z nich poskládala velkou krychli a chvíli počkala, než se sýrové krychličky k sobě přilepily. Potom z každé stěny velké krychle vyhryzla střední krychličku. Poté snědla i krychličku, která byla v - Inflace
 Kde bylo, tam bylo, car vlastnil tiskárnu na peníze a tlačil a tlačil. Výsledkem tištění peněz bylo že v prvním roce ceny stouply o 2,1%, ve druhém o 4,2%, ve třetím o 4,1% a ve čtvrtém roce vládnutí o 5,5%. Pak už car nebyl zvolen. Vypočtěte průměrnou ro
Kde bylo, tam bylo, car vlastnil tiskárnu na peníze a tlačil a tlačil. Výsledkem tištění peněz bylo že v prvním roce ceny stouply o 2,1%, ve druhém o 4,2%, ve třetím o 4,1% a ve čtvrtém roce vládnutí o 5,5%. Pak už car nebyl zvolen. Vypočtěte průměrnou ro - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
