Rovnice
Vyřeš soustavu rovnic dosazovací, porovnávací i sčítací metodou a proveď zkoušku:
4x+y=5
3x-5y=21
4x+y=5
3x-5y=21
Správná odpověď:

Tipy na související online kalkulačky
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Soustava rovnic
 Vyřeš soustavu rovnic libovolnou metodou a proveď zkoušku: 2(x+y)-3(y+2)= -1 x+2/3y-6=2
Vyřeš soustavu rovnic libovolnou metodou a proveď zkoušku: 2(x+y)-3(y+2)= -1 x+2/3y-6=2 - Priamky 2
 Vyřeš soustavu grafickou metodou: x+y=8 2x-y=1
Vyřeš soustavu grafickou metodou: x+y=8 2x-y=1 - Prosím 5
 Prosím, stanov podmínky řešitelnosti rovnice, vyřeš rovnici a proveď zkoušku, x lomeno x na druhou mínus 2x plus1 to celé mínus x+3 lomeno x na druhou mínus 1 to celé rovná se 0 x/(x²-2x+1) - (x+3)/( x²-1) = 0
Prosím, stanov podmínky řešitelnosti rovnice, vyřeš rovnici a proveď zkoušku, x lomeno x na druhou mínus 2x plus1 to celé mínus x+3 lomeno x na druhou mínus 1 to celé rovná se 0 x/(x²-2x+1) - (x+3)/( x²-1) = 0 - Eliminační metoda
 Řešte soustavu lineárních rovnic eliminační metodou: 5/2x + 3/5y= 4/15 1/2x + 2/5y= 2/15
Řešte soustavu lineárních rovnic eliminační metodou: 5/2x + 3/5y= 4/15 1/2x + 2/5y= 2/15
- Substituční 83016
 Vyřešte rovnice, najděte neznámé proměnné substituční nebo sčítací metodou: x + 3y = 19 5x + 3r = 35
Vyřešte rovnice, najděte neznámé proměnné substituční nebo sčítací metodou: x + 3y = 19 5x + 3r = 35 - Zkouška rovnice
 Řešte rovnici a proved´te zkoušku: a) 3(5-2x) + 5x = 5 -3 (x -1) b) 2(4y + 3) -3 = 2 - 5 (1 - y)
Řešte rovnici a proved´te zkoušku: a) 3(5-2x) + 5x = 5 -3 (x -1) b) 2(4y + 3) -3 = 2 - 5 (1 - y) - Soustava
 Vyřeš soustavu: (x+5)(y-2)=(x-1)(y+1) (x+1)(y+1)=(x+5)(y-1)
Vyřeš soustavu: (x+5)(y-2)=(x-1)(y+1) (x+1)(y+1)=(x+5)(y-1) - Soustava rovnic
 Řešte soustavu rovnic: x+y = -1 x+5y = 3
Řešte soustavu rovnic: x+y = -1 x+5y = 3 - Soustava rovnic
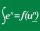 Řešte soustavu rovnic: x+4y = -1 y = -1
Řešte soustavu rovnic: x+4y = -1 y = -1
- Vyrešte
 Vyrešte nasledujíci soustavu rovnic: x + 4y = 5 2x – 3y = -6
Vyrešte nasledujíci soustavu rovnic: x + 4y = 5 2x – 3y = -6 - Soustava rovnic
 Řešte soustavu rovnic: x+y = 4 x-3y = -6
Řešte soustavu rovnic: x+y = 4 x-3y = -6 - Rovnice o dvou neznámých
 Rěšte soustavu: 15x+30y=-20 0,3x-0,2y=0,4
Rěšte soustavu: 15x+30y=-20 0,3x-0,2y=0,4 - Číselný had
 Vytvoř z rovnice číselného hada a vyřeš: 2x - 5 = 7 4x+1/3 = 7 3(x-2)+4 = 7
Vytvoř z rovnice číselného hada a vyřeš: 2x - 5 = 7 4x+1/3 = 7 3(x-2)+4 = 7 - Soustava 4R
 Řešte soustavu rovnic o čtyřech neznámých: 2a+2b-c+d=4 4a+3b-c+2d=6 8a+5b-3c+4d=12 3a+3b-2c+2d=6
Řešte soustavu rovnic o čtyřech neznámých: 2a+2b-c+d=4 4a+3b-c+2d=6 8a+5b-3c+4d=12 3a+3b-2c+2d=6
