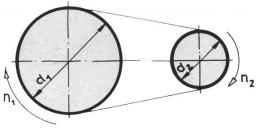
Klínový řemen
Vypočítejte délku klínového řemene pokud průměr řemenic je:
d1 = 600mm
d2 = 120mm
d = 480mm (vzdálenost os řemenic)
d1 = 600mm
d2 = 120mm
d = 480mm (vzdálenost os řemenic)
Správná odpověď:
Zobrazuji 6 komentářů:
Žák
Výše uvedené řešení vychází z chybného předpokladu, že tečna obou kružnic má stejný sklon ke spojnici středů řemenic jako spojnice průsečíků svislic procházejících středy s kružnicemi. Jinými slovy tečna není rovnoběžná s úsečkou ve výpočtu označenou jako "b". Pochopitelně je tedy chybně určen i úhel "A".
Dr Math
uhel A je uhel tecny vzhledem k spojnici stredu. body dotyku a stredy kruznic S1,S2 formuji pravouhlej lichobeznik, ktery lze rozlozit na obdelnik a pravouhly trojuhelnik. Pravouhlej trojuhelnik ma take uhel A, stranu d = |S1S2| a stranu r1-r2. Tecna je rovnobezna s useckou "b" (dlzka rovne casti remene)...
Proc by take nebyla, kdyz v bodech dotyku je tecna kolma na r1 ale take na r2, tudiz formuje se tam obdelnik o stranach b a r1.
Dejte padnejsi argument.
Proc by take nebyla, kdyz v bodech dotyku je tecna kolma na r1 ale take na r2, tudiz formuje se tam obdelnik o stranach b a r1.
Dejte padnejsi argument.
Dr Math
fuu to dalo namahu nakreslit to. Nicmene nechapu zloute primke s, a aj jinym zlutym primkam. Nemaji zaden smysl. Dulezity je jeno pravouhlej lichobeznik T1T2S2S1. tam je zrejme ze T1S1 je rovnobezne s T2S2. uhel fi = S2PT1 je proste stejny ako uhel spojnici středů řemenic jako spojnice průsečíků svislic procházejících středy s kružnicemi
Žák
No, měl jsem za to, že z obrázku v odkazu je zcela zřejmé, že tečna „t“, pochopitelně procházející body T1, T2, není rovnoběžná s přímkou „s” procházející průsečíky kružnic se svislicemi procházejícími středy. Důkazem budiž třeba to, pominuli již zmiňované analytické řešení, že v pravoúhlém trojúhelníku o stranách d, a, b = |T1T2|, z něhož správně počítáte velikost |T1T2|, musí být příslušný vnitřní úhel pí/6 rad nikoli 0,4636 rad.
Vít
No nevím, také mi to nějak nesedí. Výpočet a použití úhlu A je dost divné. Podle mne ty oblouky jsou 240° a 120°. A výsledek je tedy cca 2214 mm.
3 roky 1 Like
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- geometrie
- podobnost trojúhelníků
- planimetrie
- pravoúhlý trojúhelník
- kruh, kružnice
- trojúhelník
- lichoběžník
- kruhová výseč
- kruhový oblouk
- goniometrie a trigonometrie
- sinus
- tangens
- arkussinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Tramvajová úloha
 Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15. - Triangulace - výškové úhly
 Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž?
Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž? - Triangulace
 Zjisti výšku věže, když bylo naměřeno α=34° 30´ β=41°. Vzdálenost míst AB je 14 metrů.
Zjisti výšku věže, když bylo naměřeno α=34° 30´ β=41°. Vzdálenost míst AB je 14 metrů. - Jiho-západ
 Muž v poušti ujede 8,7 míle ve směru S 26° W (jiho-západ). Potom se otočí o 90° a přejde 9 mil ve směru na N 49° W (severo západně). Jak daleko je v té době od svého výchozího bodu a jeho postoj od jeho výchozího bodu?
Muž v poušti ujede 8,7 míle ve směru S 26° W (jiho-západ). Potom se otočí o 90° a přejde 9 mil ve směru na N 49° W (severo západně). Jak daleko je v té době od svého výchozího bodu a jeho postoj od jeho výchozího bodu? - Z věže
 Z věže 15m vysoké a od řeky 30 m se jevila šířka řeky v úhlu 15°. Jak široká je řeka v tomto místě?
Z věže 15m vysoké a od řeky 30 m se jevila šířka řeky v úhlu 15°. Jak široká je řeka v tomto místě? - Budova 3
 Budova vysoká 15 m je vzdálená od břehu řeky 30 m. Ze střechy této budovy je vidět šířku řeky pod úhlem 15°. Jak je řeka široká?
Budova vysoká 15 m je vzdálená od břehu řeky 30 m. Ze střechy této budovy je vidět šířku řeky pod úhlem 15°. Jak je řeka široká? - Po vodorovné
 Po vodorovné trati jede auto stálou rychlostí 20 m∙s–1. Prší. Kapky deště padají ve svislém směru rychlostí o velikosti 6 m∙s–1. a) Jak velká je rychlost kapek vzhledem k oknům auta? b) Jaký úhel svírají stopy dešťových kapek na okně auta se svislým směre
Po vodorovné trati jede auto stálou rychlostí 20 m∙s–1. Prší. Kapky deště padají ve svislém směru rychlostí o velikosti 6 m∙s–1. a) Jak velká je rychlost kapek vzhledem k oknům auta? b) Jaký úhel svírají stopy dešťových kapek na okně auta se svislým směre - Roviny bočních stěn
 Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’
Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Vypočítejte 53
 Vypočítejte výšku v rovnoramenném lichoběžníku, je-li obsah 520 cm² a základny a=25 cm a c=14cm. Vypočítejte vnitřní úhly lichoběžníku.
Vypočítejte výšku v rovnoramenném lichoběžníku, je-li obsah 520 cm² a základny a=25 cm a c=14cm. Vypočítejte vnitřní úhly lichoběžníku. - Tři sloupy
 Vedle přímé cestě jsou tři sloupy vysoké 6 m ve stejné vzdálenosti 10 m. Pod jakým zorným úhlem vidí Vlado každý sloup, pokud je od prvního ve vzdálenosti 30 m a jeho oči jsou ve výšce 1,8 m?
Vedle přímé cestě jsou tři sloupy vysoké 6 m ve stejné vzdálenosti 10 m. Pod jakým zorným úhlem vidí Vlado každý sloup, pokud je od prvního ve vzdálenosti 30 m a jeho oči jsou ve výšce 1,8 m? - Procentní 43321
 Kolik procentní stoupání je třeba uvést na značku, pokud úhel sklonu cesty je 6° 25´?
Kolik procentní stoupání je třeba uvést na značku, pokud úhel sklonu cesty je 6° 25´? - Podstavou
 Podstavou čtyřbokého hranolu je obdélník o rozměrech 3 dm a 4 dm. Výška hranolu je 1 m. Zjistěte jaký úhel svíra tělesová úhlopříčka s úhlopříčkou podstavy.
Podstavou čtyřbokého hranolu je obdélník o rozměrech 3 dm a 4 dm. Výška hranolu je 1 m. Zjistěte jaký úhel svíra tělesová úhlopříčka s úhlopříčkou podstavy. - Těleso
 Těleso se klouže dolů po nakloněné rovině svírající s vodorovnou rovinou úhel α = π / 4 = 45° za účinku sil tření se zrychlením a = 2,4 m/s². Pod jakým úhlem β musí být nakloněná rovina, aby se těleso po ní klouzaly po malém postrčení konstantní rychlostí
Těleso se klouže dolů po nakloněné rovině svírající s vodorovnou rovinou úhel α = π / 4 = 45° za účinku sil tření se zrychlením a = 2,4 m/s². Pod jakým úhlem β musí být nakloněná rovina, aby se těleso po ní klouzaly po malém postrčení konstantní rychlostí - Vypočtěte 10
 Vypočtěte velikost odchylky tělesové úhlopřičky a boční hrany c kvádru o rozměrech: a=28cm, b=45cm a c=73cm. Dále vypočtěte velikost odchylky tělesové úhlopřičky od roviny podstavy.
Vypočtěte velikost odchylky tělesové úhlopřičky a boční hrany c kvádru o rozměrech: a=28cm, b=45cm a c=73cm. Dále vypočtěte velikost odchylky tělesové úhlopřičky od roviny podstavy. - Pravidelný 8
 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Vzdálenost bodů
 Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S.
Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S. - Cesta
 Na cestě je značka pro stoupání s úhlem 7%. Vypočtěte pod jakým úhlem (v stupních) cesta stoupá (klesá).
Na cestě je značka pro stoupání s úhlem 7%. Vypočtěte pod jakým úhlem (v stupních) cesta stoupá (klesá).
