Z8–I–1 2017 Číslo milion
Vyjádřete číslo milion (1000000) pomocí čísel obsahujících pouze číslice 9 a algebraických operací plus, minus, krát, děleno, mocnina a odmocnina. Určete alespoň tři různá řešení.
Správná odpověď:

Zobrazuji 9 komentářů:
Dr Math
myslime jsi ze odbouravame stres u zaku... nekteri i po shlednuti vysledku a mozneho reseni prikladu MO nevi, nechapou.... Sami se rozhodnou ci se resenim inspirujou nebo to zabalej.
Nekterym zakum chybi pouze natuknuti.....
Nekterym zakum chybi pouze natuknuti.....
žák
Díky moc ! Určitě to není nic těžkého, ale zabírá to čas který né všichni mají. Ještě jedno děkuji za pomoc.
6 let 1 Like
Alice
Prosím vysvetlite mi ten 3 výsledek jaké znaménko je tam kde začínají ty malé devitky? Děkuji předem
6 let 1 Like
Žák
Můj kamarád to takhle udělal, a u 2. řešení mu řekli že se v tomto příkladě nesmí používat více devítek u sebe, pouze samostatně. Jste si svým výsledkem jistí na 100 procent?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Z7–I–1 MO 2018
 Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné číslo poskládané z těchto kartiček je dělitelné šesti. Navíc lze z těchto kartiček poskládat trojmístné číslo
Na každé ze tří kartiček je napsána jedna číslice různá od nuly (na různých kartičkách nejsou nutně různé číslice). Víme, že jakékoli trojmístné číslo poskládané z těchto kartiček je dělitelné šesti. Navíc lze z těchto kartiček poskládat trojmístné číslo - Znaménka
 5 5 5 5= 15 doplň znaménka plus minus krať děleno a 2 závorky
5 5 5 5= 15 doplň znaménka plus minus krať děleno a 2 závorky - Neznámými: 50403
 Dělení zlomků s neznámými: Zlomek 1: Množství x na druhou plus 6 krát x plus 9 nad množství x minus 1. Zlomek 2: množství x na druhou minus 9 oproti množství x na druhou minus 2 krát x plus 1. Najděte zlomek 1 nad zlomkem 2.
Dělení zlomků s neznámými: Zlomek 1: Množství x na druhou plus 6 krát x plus 9 nad množství x minus 1. Zlomek 2: množství x na druhou minus 9 oproti množství x na druhou minus 2 krát x plus 1. Najděte zlomek 1 nad zlomkem 2. - 32+2[5×(24-6)]-48÷24 11961
 Vyhodnoťte výraz: 32+2[5×(24-6)]-48÷24 Dávejte pozor na pořadí operací včetně celých čísel.
Vyhodnoťte výraz: 32+2[5×(24-6)]-48÷24 Dávejte pozor na pořadí operací včetně celých čísel. - Součin 3108
 Součin 3 čísel je 42. První je 1,5krát větší než druhé číslo a třetí je 3,5krát větší než druhé číslo. O která čísla se jedná?
Součin 3 čísel je 42. První je 1,5krát větší než druhé číslo a třetí je 3,5krát větší než druhé číslo. O která čísla se jedná? - Vypočítejte 3818
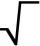 Máme 2 čísla. Kdybychom vynásobili třetí odmocninu prvního čísla s druhou odmocninou druhého čísla, dostali bychom číslo 18. Určete tato 2 čísla. Pokud má úloha v množině reálných čísel nekonečně mnoho řešení, vypočítejte jen celočíselné řešení.
Máme 2 čísla. Kdybychom vynásobili třetí odmocninu prvního čísla s druhou odmocninou druhého čísla, dostali bychom číslo 18. Určete tato 2 čísla. Pokud má úloha v množině reálných čísel nekonečně mnoho řešení, vypočítejte jen celočíselné řešení. - Krychle
 Jedna krychle je kouli vepsána a druhá opsána. Vypočítejte rozdíl objemů v obou krychlích, pokud rozdíl jejich povrchů je 231 dm².
Jedna krychle je kouli vepsána a druhá opsána. Vypočítejte rozdíl objemů v obou krychlích, pokud rozdíl jejich povrchů je 231 dm². - Odmocnina 3838
 Určete přirozené číslo, jehož druhá mocnina je 27krát větší než jeho druhá odmocnina.
Určete přirozené číslo, jehož druhá mocnina je 27krát větší než jeho druhá odmocnina. - Platilo: 7297
 Doplň symboly operací (+-*/) aby platilo: (4 4) (4 4)=15
Doplň symboly operací (+-*/) aby platilo: (4 4) (4 4)=15 - Úhlopříčka 15
 Vypočítejte objem krychle, jejíž tělesová úhlopříčka má velikost 75 dm. Načrtněte si obrázek a tělesovou úhlopříčku barevně zvýrazněte.
Vypočítejte objem krychle, jejíž tělesová úhlopříčka má velikost 75 dm. Načrtněte si obrázek a tělesovou úhlopříčku barevně zvýrazněte. - K-ciferných 7014
 Určete počet všech k-ciferných přirozených čísel, ve kterých dekadickém zápisu není 0 a jsou v něm nebo číslice sudé nebo číslice liché, vždy každá alespoň jednou.
Určete počet všech k-ciferných přirozených čísel, ve kterých dekadickém zápisu není 0 a jsou v něm nebo číslice sudé nebo číslice liché, vždy každá alespoň jednou. - Operace 4
 Operace * (hviezdička) přiřazujíci dvěma dvojicím čísel jedno číslo je zavedena takto: (a, b)*(c, d) = ac+bd víme že: (x,2)*(-1, v) = -1 a (2,-1)*(u, v)=5 a (u, v)*(1,1)=-2 Čemu je rovno (1,2)*(x, y) jesliže y=3?
Operace * (hviezdička) přiřazujíci dvěma dvojicím čísel jedno číslo je zavedena takto: (a, b)*(c, d) = ac+bd víme že: (x,2)*(-1, v) = -1 a (2,-1)*(u, v)=5 a (u, v)*(1,1)=-2 Čemu je rovno (1,2)*(x, y) jesliže y=3? - 3x^2+bx+c=0 82539
 V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce.
V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce. - Neznámých 50681
 Součin dvou neznámých čísel jsou dvě setiny. První číslo je 1,25krát větší než druhé číslo. Určete obě čísla.
Součin dvou neznámých čísel jsou dvě setiny. První číslo je 1,25krát větší než druhé číslo. Určete obě čísla. - Rovnice s absolutní hodnotou
 Kolik řešení má rovnice (|x| +x) |x-3| = |x+1| v oboru reálných čísel?
Kolik řešení má rovnice (|x| +x) |x-3| = |x+1| v oboru reálných čísel? - MO 2019 Z9–I–5
 Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Majka vy
Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Majka vy - Tří čísla
 Společný násobek tří čísel je 3276. Jedno číslo se v něm nachází 63krát, druhé 7krát a třetí 9krát. Které jsou to čísla?
Společný násobek tří čísel je 3276. Jedno číslo se v něm nachází 63krát, druhé 7krát a třetí 9krát. Které jsou to čísla?
