Sto známek
Je sto dopisních známek a stojí sto korun. Jsou tam známky dvacetiháléřové, korunové, dvojkorunové a pětikorunové. Kolik je kterých? Kolik má úloha řešení?
Správná odpověď:

Tipy na související online kalkulačky
Řešíte Diofantovské problémy a hledáte kalkulačku diofantovských celočíselných rovnic?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Poštovní známky
 V zásuvce psacího stolu bylo 301 poštovních známek. Byly to známky za 2,3 a 5 korun. Počet každého druhu lze zapsat trojciferným číslem. Celková cena všech známek je 1003 Kč. Kolik bylo kterých známek?
V zásuvce psacího stolu bylo 301 poštovních známek. Byly to známky za 2,3 a 5 korun. Počet každého druhu lze zapsat trojciferným číslem. Celková cena všech známek je 1003 Kč. Kolik bylo kterých známek? - Sekretářka
 Sekretářka firmy nakoupila známky v hodnotě 20 Kč a v hodnotě 15 Kč. Celkový počet koupených známek je 120 a sekretářka platila celkem 2265 Kč. Kolik koupila známek v hodnotě 15 Kč?
Sekretářka firmy nakoupila známky v hodnotě 20 Kč a v hodnotě 15 Kč. Celkový počet koupených známek je 120 a sekretářka platila celkem 2265 Kč. Kolik koupila známek v hodnotě 15 Kč? - Pokladnička
 Lucie má v pokladničce pouze dvoukorunové a pětikorunové mince. Celkem má 30 mincí v hodnotě 108 korún. Kolik má dvoukorunových a kolik pětikorunových mincí?
Lucie má v pokladničce pouze dvoukorunové a pětikorunové mince. Celkem má 30 mincí v hodnotě 108 korún. Kolik má dvoukorunových a kolik pětikorunových mincí? - Známky
 Tibor má 4 krát více známek než Miro a 7krát více než Stano. Kolik známek mají všichni tři spolu, pokud Tibor má 504 známek?
Tibor má 4 krát více známek než Miro a 7krát více než Stano. Kolik známek mají všichni tři spolu, pokud Tibor má 504 známek?
- Radek 2
 Radek měl ve sbírce známek polovinu známek českých, třetinu slovenských a právě 128 zámořských. Jiné známky Radek nesbíral. Vypočtěte, kolik známek měl celkem Radek ve sbírce.
Radek měl ve sbírce známek polovinu známek českých, třetinu slovenských a právě 128 zámořských. Jiné známky Radek nesbíral. Vypočtěte, kolik známek měl celkem Radek ve sbírce. - Interpretujte 82345
 Petrovy známky v jejím třetím periodickém testu jsou 98, 97, 86, 94, 90, 97, 91 a 94. Najděte medián jeho známek a interpretujte výsledek.
Petrovy známky v jejím třetím periodickém testu jsou 98, 97, 86, 94, 90, 97, 91 a 94. Najděte medián jeho známek a interpretujte výsledek. - Stokrát 4471
 Juraj začal sbírat známky, už jich má 36. Jeho kamarád Šimon sbírá známky 12 let, ve svých albech jich má stokrát více než Juraj. Kolik známek má Šimon?
Juraj začal sbírat známky, už jich má 36. Jeho kamarád Šimon sbírá známky 12 let, ve svých albech jich má stokrát více než Juraj. Kolik známek má Šimon? - Zvířátky 2191
 role a, Anička má 14 známek se zvířátky. Je to proto, že dnes ráno dala Vierke 3 známky s opicemi. Kolik známek se zvířátky měla předtím? role b, Večer Anička vyměnila 4 známky se lvy za 2 známky s opicemi. Kolik známek se zvířátky měla po výměně?
role a, Anička má 14 známek se zvířátky. Je to proto, že dnes ráno dala Vierke 3 známky s opicemi. Kolik známek se zvířátky měla předtím? role b, Večer Anička vyměnila 4 známky se lvy za 2 známky s opicemi. Kolik známek se zvířátky měla po výměně? - Střádaní
 Jana střádá dvoukorunové a pětikorunové mince. V pokladničce má 10 mincí. Kolik je dvoukorunových a kolik pětikorunových, jestliže má našetřeno 29 Kč?
Jana střádá dvoukorunové a pětikorunové mince. V pokladničce má 10 mincí. Kolik je dvoukorunových a kolik pětikorunových, jestliže má našetřeno 29 Kč?
- Aritmetický 64394
 Karolína nechce doma prozradit, jaké známky bude mít na vysvědčení. Řekla jen toto: „Na vysvědčení bude 8 známek, jejich aritmetický průměr je 2,125, medián je 2, modus 1 a nebudu mít žádnou dvojku. Kolik čtyřek bude mít Karolína na vysvědčení?
Karolína nechce doma prozradit, jaké známky bude mít na vysvědčení. Řekla jen toto: „Na vysvědčení bude 8 známek, jejich aritmetický průměr je 2,125, medián je 2, modus 1 a nebudu mít žádnou dvojku. Kolik čtyřek bude mít Karolína na vysvědčení? - V rovině
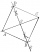 V rovině jsou dány 3 různé body C, E, F. Dorýsuj prosím čtverec ABCD, když E, F leží na úhlopříčkách tohoto čtverce. Kolik má úloha řešení? Děkuji
V rovině jsou dány 3 různé body C, E, F. Dorýsuj prosím čtverec ABCD, když E, F leží na úhlopříčkách tohoto čtverce. Kolik má úloha řešení? Děkuji - Kulky a kuličky
 Chlapci si měnili známky, kuličky a míčky. Za 9 kuliček je 3 známek, za 2 míčků je 44 známek. Kolik kuliček je za 1 míček?
Chlapci si měnili známky, kuličky a míčky. Za 9 kuliček je 3 známek, za 2 míčků je 44 známek. Kolik kuliček je za 1 míček? - Kto dnes šetri
 Jana střadá dvoukorunové a pětikorunové mince. V pokladničce má 32 mincí. Kolik je dvoukorunových a kolik pětikorunových, jestliže má našetřeno 145 korun?
Jana střadá dvoukorunové a pětikorunové mince. V pokladničce má 32 mincí. Kolik je dvoukorunových a kolik pětikorunových, jestliže má našetřeno 145 korun? - Slovní úlohy o směsích
 Petra má dvoukorunové a pětikorunové mince. V pokladničce má 10 mincí. Kolik má dvoukorun a kolik pětikorun, jestliže si uspořila 29 Kč?
Petra má dvoukorunové a pětikorunové mince. V pokladničce má 10 mincí. Kolik má dvoukorun a kolik pětikorun, jestliže si uspořila 29 Kč?
- Známky
 Vašek má 62 známek, Libor má 71 známek. Oba chlapci si spolu známky měnili. Vašek chtěl od Libora 2 velmi vzácné známky. Libor mu je vyměnil, ale Vašek mu musel za každou z těchto dvou známek dát 2 jiné. Kolik pak měl každý z nich známek?
Vašek má 62 známek, Libor má 71 známek. Oba chlapci si spolu známky měnili. Vašek chtěl od Libora 2 velmi vzácné známky. Libor mu je vyměnil, ale Vašek mu musel za každou z těchto dvou známek dát 2 jiné. Kolik pak měl každý z nich známek? - Vyměňovaly 78484
 Kamila a Kristýna si vyměňovaly známky. Kristýna dala Kamile při této výměně 24 známek. Po výměně měla Kamila o 7 známek méně než na začátku. Kolik známek dala při této výměně Kamila Kristýně?
Kamila a Kristýna si vyměňovaly známky. Kristýna dala Kamile při této výměně 24 známek. Po výměně měla Kamila o 7 známek méně než na začátku. Kolik známek dala při této výměně Kamila Kristýně? - Dvoueurových 6035
 Chlapec si koupil známky v hodnotě 2 € a 3 € v celkové hodnotě 65 €. Dvoueurových bylo 5 krát více než tříeurových. Kolik bylo jakých známek?
Chlapec si koupil známky v hodnotě 2 € a 3 € v celkové hodnotě 65 €. Dvoueurových bylo 5 krát více než tříeurových. Kolik bylo jakých známek?
