Z9–I–3 - 2017 kafemlýnky2
Roboti Robert a Hubert skládají a rozebírají kafemlýnky. Přitom každý z nich kafemlýnek složí čtyřikrát rychleji, než jej sám rozebere. Když ráno přišli do dílny, několik kafemlýnků už tam bylo složeno. V 7:00 začal Hubert skládat a Robert rozebírat, přesně ve 12:00 Hubert dokončil skládání kafemlýnku a Robert rozebírání jiného. Celkem za tuto směnu přibylo 70 kafemlýnků.
Ve 13:00 začal Robert skládat a Hubert rozebírat, přesně ve 22:00 dokončil Robert skládání posledního kafemlýnku a Hubert rozebírání jiného. Celkem za tuto směnu přibylo 36 kafemlýnků.
Za jak dlouho by složili 360 kafemlýnků, pokud by Robert i Hubert skládali společně?
PS. pozor na podobny priklad https://www.hackmath.net/cz/priklad/5417?result=10
Ve 13:00 začal Robert skládat a Hubert rozebírat, přesně ve 22:00 dokončil Robert skládání posledního kafemlýnku a Hubert rozebírání jiného. Celkem za tuto směnu přibylo 36 kafemlýnků.
Za jak dlouho by složili 360 kafemlýnků, pokud by Robert i Hubert skládali společně?
PS. pozor na podobny priklad https://www.hackmath.net/cz/priklad/5417?result=10
Správná odpověď:

Zobrazuji 17 komentářů:
Dr Math
urcite, nějakou fintickou, ktera vlastně jen simuluje soustavu dvou rovnic o 2 neznámých ....
Hugo
Jestli se mihu zeptat, proc je tam deleno 4? ("r/4") To je proto, že je 4x rychlejší jak rozebírání?
Dr Math
r - h/4 je vyjadreni celkoveho hodinoveho vykonu dilny= Robert sklada a Hubert rozobera ctvrtinovou rychlosti
h - r/4 - celkoveho hodinoveho vykonu dilny, akurat ze rozobera Robert a Hubert sklada
h - r/4 - celkoveho hodinoveho vykonu dilny, akurat ze rozobera Robert a Hubert sklada
Žák
Nechapu jak vam mohlo h=8 a r=16 , když jsem to počitala, tak mi vyšel vysledek h=4 a r=14 a to pomoci vypočtu: 70:5=14 a 36:9=4. Pořad se snažim to vypočitat tak, aby vysledek vyšel stejně, ale pořad mi to nejde
Tipy na související online kalkulačky
Chceš si vypočítat nejmenší společný násobek dvou nebo více čísel?
Chceš si vypočítat největší společný dělitel dvou nebo více čísel?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotky času, např. hodiny na minuty?
Chceš si vypočítat největší společný dělitel dvou nebo více čísel?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotky času, např. hodiny na minuty?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- rovnice
- soustava rovnic
- prvočísla
- dělitelnost
- nejmenší společný násobek (NSN)
- největší společný dělitel (NSD)
- základní funkce
- úvaha
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Aritmeticka i geometrická
 Tři čísla, které tvoří aritmetickou posloupnost, mají součet 30. Pokud odečteme od prvního 5, od druhého 4 a třetí ponecháme, dostaneme geometrickou posloupnost. Urči členy AP i GP.
Tři čísla, které tvoří aritmetickou posloupnost, mají součet 30. Pokud odečteme od prvního 5, od druhého 4 a třetí ponecháme, dostaneme geometrickou posloupnost. Urči členy AP i GP. - Slávkine čísla
 Slávka si napsala barevnými fixy čtyři různé přirozená čísla: červené, modré, zelené a žluté. Když červené číslo vydělí modrým, dostane jako neúplný podíl zelené číslo a žluté představuje zbytek po tomto dělení. Když vydělí modré číslo zeleným, vyjde její
Slávka si napsala barevnými fixy čtyři různé přirozená čísla: červené, modré, zelené a žluté. Když červené číslo vydělí modrým, dostane jako neúplný podíl zelené číslo a žluté představuje zbytek po tomto dělení. Když vydělí modré číslo zeleným, vyjde její - V hotelu
 V hotelu Holiday mají na každém patře stejný počet pokojů. Pokoje jsou číslovány přirozenými čísly postupně od prvního patra, žádné číslo není vynecháno a každý pokoj má jiné číslo. Do hotelu přicestovali tři turisté. První se ubytoval v pokoji číslo 50 n
V hotelu Holiday mají na každém patře stejný počet pokojů. Pokoje jsou číslovány přirozenými čísly postupně od prvního patra, žádné číslo není vynecháno a každý pokoj má jiné číslo. Do hotelu přicestovali tři turisté. První se ubytoval v pokoji číslo 50 n - Určete 46
 Určete čtyři čísla tak, aby první tři tvořila tři následující členy aritmetické posloupnosti s diferencí d=-3 a poslední tři tvořila následující členy geometrické posloupnosti s qvocientem q=jedna polovina.
Určete čtyři čísla tak, aby první tři tvořila tři následující členy aritmetické posloupnosti s diferencí d=-3 a poslední tři tvořila následující členy geometrické posloupnosti s qvocientem q=jedna polovina.
- GP složité
 Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: a1 = 5, an = 320, sn = 635, n=?, q=?
Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: a1 = 5, an = 320, sn = 635, n=?, q=? - Konečná posloupnost
 Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: a1=18, an=13122, sn=19674, n=?, q=?
Určete zbývající veličiny v konečné geometrické posloupnosti, je-li dáno: a1=18, an=13122, sn=19674, n=?, q=? - Geometrická
 Geometrická posloupnost se šesti členy má součet všech šesti členů rovnající se 63; součet sudých členů má hodnotu 42. Určete tyto členy.
Geometrická posloupnost se šesti členy má součet všech šesti členů rovnající se 63; součet sudých členů má hodnotu 42. Určete tyto členy. - Odečteme-li 46781
 Odečteme-li od čísel 33, 45 a 63 totéž číslo, dostaneme tři za sebou jdoucí členy GP. Určete tuto GP a vypočítejte její pátý člen.
Odečteme-li od čísel 33, 45 a 63 totéž číslo, dostaneme tři za sebou jdoucí členy GP. Určete tuto GP a vypočítejte její pátý člen. - Povrch pláště , objem
 V rotačním válci je dáno: povrch pláště (bez podstav) S = 96 cm² a objem V = 192 cm krychlových. Vypočítejte poloměr a výšku tohoto válce.
V rotačním válci je dáno: povrch pláště (bez podstav) S = 96 cm² a objem V = 192 cm krychlových. Vypočítejte poloměr a výšku tohoto válce.
- V rotačním válci
 V rotačním válci je dáno: povrch S = 96 cm² a objem V = 192 cm krychlových. Vypočtěte jeho poloměr a výšku.
V rotačním válci je dáno: povrch S = 96 cm² a objem V = 192 cm krychlových. Vypočtěte jeho poloměr a výšku. - Stěnové úhlopříčky
 Pokud jsou stěnové úhlopříčky kvádru x, y a z (diagonály), pak najděte objem kvádru. Vyřešte pro x = 1,5, y = 2, z = 1,8
Pokud jsou stěnové úhlopříčky kvádru x, y a z (diagonály), pak najděte objem kvádru. Vyřešte pro x = 1,5, y = 2, z = 1,8 - Dve tětivy
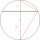 Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm.
Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm. - MO Z9-I-6 2019
 Kristýna zvolila jisté liché přirozené číslo dělitelné třemi. Jakub s Davidem pak zkoumali trojúhelníky, které mají obvod v milimetrech roven Kristýnou zvolenému číslu a jejichž strany mají délky v milimetrech vyjádřeny navzájem různými celými čísly. Jaku
Kristýna zvolila jisté liché přirozené číslo dělitelné třemi. Jakub s Davidem pak zkoumali trojúhelníky, které mají obvod v milimetrech roven Kristýnou zvolenému číslu a jejichž strany mají délky v milimetrech vyjádřeny navzájem různými celými čísly. Jaku - Gramáže v kuchařce (Matik)
 V kuchařce od Matěje Matemakaka se psalo: největší společný dělitel gramáže mouky a gramáže cukru je 15, největší společný dělitel gramáže cukru a gramáže citronové kůry je 6, součin gramáže cukru a gramáže citrónové kůry je 1800, nejmenší společný násobe
V kuchařce od Matěje Matemakaka se psalo: největší společný dělitel gramáže mouky a gramáže cukru je 15, největší společný dělitel gramáže cukru a gramáže citronové kůry je 6, součin gramáže cukru a gramáže citrónové kůry je 1800, nejmenší společný násobe
- V Kocourkově - Z8-I-6 2019 MO
 V Kocourkově používají mince pouze se dvěma hodnotami, které jsou vyjádřeny v kocourkovských korunách kladnými celými čísly. Pomocí dostatečného množství takových mincí je možné zaplatit jakoukoli celočíselnou částku větší než 53 kocourkovských korun, a t
V Kocourkově používají mince pouze se dvěma hodnotami, které jsou vyjádřeny v kocourkovských korunách kladnými celými čísly. Pomocí dostatečného množství takových mincí je možné zaplatit jakoukoli celočíselnou částku větší než 53 kocourkovských korun, a t - GP tři členy
 Druhý a třetí člen geometrické posloupnosti jsou 24 a 12 (c +1) v tomto pořadí. Za předpokladu, že součet prvních tří členů posloupnosti je 76, určitě hodnotu c.
Druhý a třetí člen geometrické posloupnosti jsou 24 a 12 (c +1) v tomto pořadí. Za předpokladu, že součet prvních tří členů posloupnosti je 76, určitě hodnotu c. - Rovnice hyperboly
 Napište rovnici hyperboly se středem S [0; 0], která prochází body: A [5; 3] B [8; -10]
Napište rovnici hyperboly se středem S [0; 0], která prochází body: A [5; 3] B [8; -10]
