Z9-I-6 MO 2017
Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč.
Správná odpověď:

Zobrazuji 11 komentářů:
Dr Math
skuste za a například tato čísla a dostanete 4 uspořádání .... (jako v příkladu)
a1 = 1
a2 = -5
a3 = -0.75
a4 = -0.25
Totiž číselnou osu dělí zlomové body - D = {-1, -0.5, 0}, cize na 4 casti .... Ine mozne uspořádání není možné dostat. V zlomových bodech dochází k rovnosti bodů ....
a1 = 1
a2 = -5
a3 = -0.75
a4 = -0.25
Totiž číselnou osu dělí zlomové body - D = {-1, -0.5, 0}, cize na 4 casti .... Ine mozne uspořádání není možné dostat. V zlomových bodech dochází k rovnosti bodů ....
Amálie
Není mi jasné zadání, natož řešení. Například co prosím znamená uvázat navzájem různé body? Našel by se někdo kdo by to celé prosím vysvětlil?
6 let 1 Like
Dr Math
zadání se da vysvetlit tak ze najděte nějaké hodnoty "a" pro ktere jsou tři čísla a, 2a, 3a + 1 spořádaně ve třech různých pořadích .... např. pro a = 1 su ty tři cisla 1,2,4 a su uspořádaně vzestupně. pro a=-5 bude poradi zase jine vid reseni...
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Číselna os 2
 Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč.
Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč. - Mirek a Zuzka
 Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3. Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich m
Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3. Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich m - Obecná rovnice
 Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná
Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná - Rozhodněte 19893
 Rozhodněte, zda body A[-2, -5], B[4, 3] a C[16, -1] leží na stejné přímce.
Rozhodněte, zda body A[-2, -5], B[4, 3] a C[16, -1] leží na stejné přímce.
- Protíná úsečku
 Rozhodněte, zda přímka p: x + 2 y - 7 = 0 protíná úsečku danou body A [1, 1] a B [5, 3]
Rozhodněte, zda přímka p: x + 2 y - 7 = 0 protíná úsečku danou body A [1, 1] a B [5, 3] - Příslušející 82704
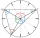 Na kruhovém ciferníku hodin navzájem pospojujeme body příslušející číslům 2,5,9, čímž vznikne trojúhelník. Vypočítejte velikosti všech vnitřních úhlů.
Na kruhovém ciferníku hodin navzájem pospojujeme body příslušející číslům 2,5,9, čímž vznikne trojúhelník. Vypočítejte velikosti všech vnitřních úhlů. - Z8-I-6 MO 2017
 Přímka představuje číselnou osu a vyznačené body odpovídají číslům a, - a, a + 1, avšak v neurčeném pořadí. Sestrojte body, které odpovídají číslům 0 a 1. Proberte všechny možnosti.
Přímka představuje číselnou osu a vyznačené body odpovídají číslům a, - a, a + 1, avšak v neurčeném pořadí. Sestrojte body, které odpovídají číslům 0 a 1. Proberte všechny možnosti. - Krabice bez víka
 Vypočítej, zda bude stačit 11 dm² papíru na slepeni krabice bez víka s rozměry dna 2 dm a 15cm a výškou 12 cm. Zapiš 0 = Ne, 1=Ano
Vypočítej, zda bude stačit 11 dm² papíru na slepeni krabice bez víka s rozměry dna 2 dm a 15cm a výškou 12 cm. Zapiš 0 = Ne, 1=Ano - Užasné číslo
 Užasným číslem nazveme takové sudé číslo, jehož rozklad na součin prvočísel má právě tři ne nutně různé činitele a součet všech jeho dělitelů je roven dvojnásobku tohoto čísla. Najděte všechna užasná čísla.
Užasným číslem nazveme takové sudé číslo, jehož rozklad na součin prvočísel má právě tři ne nutně různé činitele a součet všech jeho dělitelů je roven dvojnásobku tohoto čísla. Najděte všechna užasná čísla.
- Trojúhelníku 79314
 Na kruhovém ciferníku hodin navzájem pospojujeme body příslušející číslům 2, 9,11 čímž vznikne trojúhelník. vypočítejte velikosti všech vnitřních úhlů toho trojúhelníku.
Na kruhovém ciferníku hodin navzájem pospojujeme body příslušející číslům 2, 9,11 čímž vznikne trojúhelník. vypočítejte velikosti všech vnitřních úhlů toho trojúhelníku. - MO Z6-1-3 2017 šachovnica
 Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H
Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H - Vertikálně 81283
 Sarah a Jamal byli partnery v hodině matematiky a pracovali nezávisle. Každý z nich začal v bodě (−2, 5) a pohyboval se o 3 jednotky vertikálně v rovině. Každý student se dostal do jiného koncového bodu. Jak je to možné? Vysvětlete a uveďte dva různé konc
Sarah a Jamal byli partnery v hodině matematiky a pracovali nezávisle. Každý z nich začal v bodě (−2, 5) a pohyboval se o 3 jednotky vertikálně v rovině. Každý student se dostal do jiného koncového bodu. Jak je to možné? Vysvětlete a uveďte dva různé konc - Nejmenší 66994
 V sáčku je 180 kuliček ve třech různých barvách. Jaký nejmenší počet kuliček je třeba vybrat, aby mezi nimi byly alespoň 3 stejné barvy, pokud kuliček stejné barvy je ve všech třech barvách stejně.
V sáčku je 180 kuliček ve třech různých barvách. Jaký nejmenší počet kuliček je třeba vybrat, aby mezi nimi byly alespoň 3 stejné barvy, pokud kuliček stejné barvy je ve všech třech barvách stejně. - Pan Cuketa
 Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja
Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja
- Na mistrovství
 Na mistrovství světa 2021 v hokeji je ve skupině A 8 mužstev, každé z nich hraje 7 zápasů, v každém zápase jsou pro každé mužstvo 4 možnosti získání bodů (3-2-1-0), vždy je to ale spárované s body soupeře ( 0-1-2-3). Kolik existuje možností rozdělení bodů
Na mistrovství světa 2021 v hokeji je ve skupině A 8 mužstev, každé z nich hraje 7 zápasů, v každém zápase jsou pro každé mužstvo 4 možnosti získání bodů (3-2-1-0), vždy je to ale spárované s body soupeře ( 0-1-2-3). Kolik existuje možností rozdělení bodů - Vektorovou 18193
 Nechť v = (1, 2, 1), u = (0, -1, 3) a w = (1, 0, 7) . Vyřešte vektorovou rovnici c1 v + c2 u + c3 w = 0 pro proměnné c1, c2, c3 a rozhodněte, zda vektory v, u a w jsou lineárně závislé nebo nezávislé
Nechť v = (1, 2, 1), u = (0, -1, 3) a w = (1, 0, 7) . Vyřešte vektorovou rovnici c1 v + c2 u + c3 w = 0 pro proměnné c1, c2, c3 a rozhodněte, zda vektory v, u a w jsou lineárně závislé nebo nezávislé - Zjednodušte 82444
 Na přímce jsou tři body: A, BC. Pokud CD = 8x, DE = 3 a CE = x + 10, co je CD? Zjednodušte svou odpověď a napište ji jako správný zlomek, smíšené číslo nebo celé číslo.
Na přímce jsou tři body: A, BC. Pokud CD = 8x, DE = 3 a CE = x + 10, co je CD? Zjednodušte svou odpověď a napište ji jako správný zlomek, smíšené číslo nebo celé číslo.
