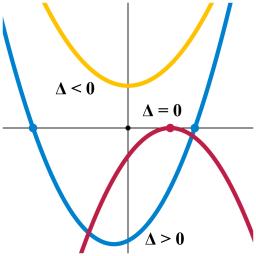
Diskriminant
Určitě diskriminant rovnice:
x2+6x+34=1
x2+6x+34=1
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Kvadratická rovnice
 Určitě čísla b, c tak aby čísla x1 = -1 a x2 = 6 byly kořeny kvadratické rovnice: 4x ² + b x + c = 0
Určitě čísla b, c tak aby čísla x1 = -1 a x2 = 6 byly kořeny kvadratické rovnice: 4x ² + b x + c = 0 - Asymptota
 Určite vertikálnu asymptotu funkcie f(x) = (-2x-8)/(2x+26).
Určite vertikálnu asymptotu funkcie f(x) = (-2x-8)/(2x+26). - Rovnice
 Rovnice -2x²+bx -100 =0 má jeden kořen x1 = 12. Určitě koeficient b a druhý kořen x2.
Rovnice -2x²+bx -100 =0 má jeden kořen x1 = 12. Určitě koeficient b a druhý kořen x2. - Rovnice:
 Rovnice: 6(x+1)-4(2x+3)=7(x-1)+5(9-x)
Rovnice: 6(x+1)-4(2x+3)=7(x-1)+5(9-x)
- Určite
 Určite uhol ϕ: ϕ + 71°15' = 90°
Určite uhol ϕ: ϕ + 71°15' = 90° - Rovnice
 Řešte rovnici a proveďte zkoušku: 2(4x + 3) - 2 = 6 - 5(1 - x)
Řešte rovnici a proveďte zkoušku: 2(4x + 3) - 2 = 6 - 5(1 - x) - Rovnice 25
 Řešte rovnice: (3n-3) / 3= (9+2n) / 2 2x/4 - 3 = 1/2x + 1
Řešte rovnice: (3n-3) / 3= (9+2n) / 2 2x/4 - 3 = 1/2x + 1 - Jednoduchá rovnice 5
 Rovnice: 2,5+x=4,1+0,7
Rovnice: 2,5+x=4,1+0,7 - Číselný had
 Vytvoř z rovnice číselného hada a vyřeš: 2x - 5 = 7 4x+1/3 = 7 3(x-2)+4 = 7
Vytvoř z rovnice číselného hada a vyřeš: 2x - 5 = 7 4x+1/3 = 7 3(x-2)+4 = 7
- Zkouška rovnice
 Řešte rovnici a proved´te zkoušku: a) 3(5-2x) + 5x = 5 -3 (x -1) b) 2(4y + 3) -3 = 2 - 5 (1 - y)
Řešte rovnici a proved´te zkoušku: a) 3(5-2x) + 5x = 5 -3 (x -1) b) 2(4y + 3) -3 = 2 - 5 (1 - y) - Rovnice jednoduchá
 Řešte následující jednoduchou rovnici: 2. (4x + 3) = 2-5. (1-x)
Řešte následující jednoduchou rovnici: 2. (4x + 3) = 2-5. (1-x) - Dve rovnice
 Riešte dve rovnice: 7*(x+1)-(3x+1)=21/2 a/3-a+6/12=2a-4
Riešte dve rovnice: 7*(x+1)-(3x+1)=21/2 a/3-a+6/12=2a-4 - Pravouhlý
 Určitě úhly pravoúhlého trojúhelníku, s přeponou c a odvesnamy a, b; jestliže platí: 2a +5b = 5,064c
Určitě úhly pravoúhlého trojúhelníku, s přeponou c a odvesnamy a, b; jestliže platí: 2a +5b = 5,064c - Přirozené 4006
 Řešte rovnici: (4x/2,5x)+(2,4:x)=3,1. x je přirozené číslo.
Řešte rovnici: (4x/2,5x)+(2,4:x)=3,1. x je přirozené číslo.
