Pravděpodobnosti
Pokud P (A) = 0,62 P (B) = 0,78 a P (A ∩ B) = 0,26, vypočítejte následující pravděpodobnosti (zjednotenia. průniků, opačných jevů a jejich kombinací):
Správná odpověď:
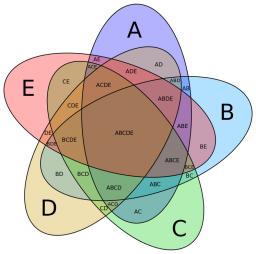
Tipy na související online kalkulačky
Chceš si dát spočítat kombinační číslo?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Rovnoramenného 36691
 Vypočítejte délku ramen a obsah rovnoramenného lichoběžníku, pokud znáte následující parametry: o = 20 cm a = 10 cm, c = 4 cm v = 2 cm
Vypočítejte délku ramen a obsah rovnoramenného lichoběžníku, pokud znáte následující parametry: o = 20 cm a = 10 cm, c = 4 cm v = 2 cm - Hod mincí
 Hodíme mincí tj. v každém hodu padne lev či panna se stejnou pravděpodobností 1/2. Určete, kolik nejméně musíme provést hodů, aby s pravděpodobností 0,9 padl lev alespoň jednou.
Hodíme mincí tj. v každém hodu padne lev či panna se stejnou pravděpodobností 1/2. Určete, kolik nejméně musíme provést hodů, aby s pravděpodobností 0,9 padl lev alespoň jednou. - Rozdelenie
 Rozdělení náhodné proměnné X je dáno následující tabulkou. Vypočítejte P[X je liché], E[X] a P[1<X≤6] Tabulka rozdělení pravděpodobnosti: xi; 1; 2; 3 ; 4; 5; 6; 7; 8; 9 pi; 0,30; 0,12; 0,18; 0,10; 0,07; 0,07; 0,06; 0,05; 0,05
Rozdělení náhodné proměnné X je dáno následující tabulkou. Vypočítejte P[X je liché], E[X] a P[1<X≤6] Tabulka rozdělení pravděpodobnosti: xi; 1; 2; 3 ; 4; 5; 6; 7; 8; 9 pi; 0,30; 0,12; 0,18; 0,10; 0,07; 0,07; 0,06; 0,05; 0,05 - Pravděpodobnost 80860
 Student při zkoušce táhne 3 otázky z 20. Je připraven na 14 z nich. Určete pravděpodobnost, že si vytáhne alespoň jednu, kterou ví.
Student při zkoušce táhne 3 otázky z 20. Je připraven na 14 z nich. Určete pravděpodobnost, že si vytáhne alespoň jednu, kterou ví. - Polopřímkách 80498
 Daný je ostroúhlý trojúhelník ABC. Na polopřímkách opačných k BA a CA leží postupně body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokažte, že střed kružnice opsané trojúhelníku ADE leží na kružnici opsané trojúhelníku ABC.
Daný je ostroúhlý trojúhelník ABC. Na polopřímkách opačných k BA a CA leží postupně body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokažte, že střed kružnice opsané trojúhelníku ADE leží na kružnici opsané trojúhelníku ABC. - Číslice
 Kolik lichých čtyřmístných čísel můžeme vytvořit z číslic 0,3,5,6,7? a) cifry se mohou opakovat b) cifry se nemohou opakovat
Kolik lichých čtyřmístných čísel můžeme vytvořit z číslic 0,3,5,6,7? a) cifry se mohou opakovat b) cifry se nemohou opakovat - Pravděpodobnost 80856
 Pravděpodobnost výskytu určitého jevu je při všech pokusech stejná a rovná se 0,7. Pokusy se opakují tak dlouho, dokud tento jev nenastane. Jaká je pravděpodobnost, že budeme muset provést pátý pokus?
Pravděpodobnost výskytu určitého jevu je při všech pokusech stejná a rovná se 0,7. Pokusy se opakují tak dlouho, dokud tento jev nenastane. Jaká je pravděpodobnost, že budeme muset provést pátý pokus? - Pravděpodobnost 24581
 Na základě předchozí kontroly je známo, že při výrobě určitého výrobku se vyskytují 3% zmetků. a) Vypočítejte pravděpodobnost jevu, že mezi 100 náhodně vybranými výrobky jsou právě 2 zmetky, přičemž každý výrobek po kontrole vrátíme do původního souboru.
Na základě předchozí kontroly je známo, že při výrobě určitého výrobku se vyskytují 3% zmetků. a) Vypočítejte pravděpodobnost jevu, že mezi 100 náhodně vybranými výrobky jsou právě 2 zmetky, přičemž každý výrobek po kontrole vrátíme do původního souboru. - CFO ředitel
 Finanční ředitel stanovil pro výnosnost nového pobočky firmy následující scénáře ziskovosti: Zisk 5 mil. Kč s pravděpodobnostní 0,1. Zisk 3 mil. Kč s pravděpodobností 0,3. Zisk 1 mil. Kč s pravděpodobností 0,4. Ztráta 2 mil. Kč s pravděpodobností 0,2. Sta
Finanční ředitel stanovil pro výnosnost nového pobočky firmy následující scénáře ziskovosti: Zisk 5 mil. Kč s pravděpodobnostní 0,1. Zisk 3 mil. Kč s pravděpodobností 0,3. Zisk 1 mil. Kč s pravděpodobností 0,4. Ztráta 2 mil. Kč s pravděpodobností 0,2. Sta - Následující 38871
 Pokud z1=5+3i a z2=4-2i, napište následující komplexní čísla ve tvaru a+bi a) 4z1+6z2 b) z1*z2
Pokud z1=5+3i a z2=4-2i, napište následující komplexní čísla ve tvaru a+bi a) 4z1+6z2 b) z1*z2 - Pravděpodobnost jevu
 Pravděpodobnost že nastane jev J při 3 nezávislých pokusech je 0,6. Jaká je pravděpodobnost, že jev J nastane při jednom pokusu (pokud při každém pokusu je pravděpodobnost stejná)?
Pravděpodobnost že nastane jev J při 3 nezávislých pokusech je 0,6. Jaká je pravděpodobnost, že jev J nastane při jednom pokusu (pokud při každém pokusu je pravděpodobnost stejná)? - Vyhovujících 82410
 Čtyři spolužáci (Ivan, Matej, Fero, Ľuboš), chodící do školy týmž tramvajovým spojem, se dohodli, že se utkají ráno na zastávce před školou. Jak si slíbili, tak se také stalo. První spolužák dorazil na zastávku před školu tramvají s příjezdem v 7:00 a pos
Čtyři spolužáci (Ivan, Matej, Fero, Ľuboš), chodící do školy týmž tramvajovým spojem, se dohodli, že se utkají ráno na zastávce před školou. Jak si slíbili, tak se také stalo. První spolužák dorazil na zastávku před školu tramvají s příjezdem v 7:00 a pos - Kroužek v škole
 27 žáků navštěvuje nějaký kroužek, taneční kroužek navštěvuje 14 žáků, sportovní 21 žáků a dramatický 16 žáků. Taneční a sportovní navštěvuje 9 žáků, taneční a dramatický 6 žáků, sportovní a dramatický 11 žáků. Kolik žáků navštěvuje všechny 3 kroužky?
27 žáků navštěvuje nějaký kroužek, taneční kroužek navštěvuje 14 žáků, sportovní 21 žáků a dramatický 16 žáků. Taneční a sportovní navštěvuje 9 žáků, taneční a dramatický 6 žáků, sportovní a dramatický 11 žáků. Kolik žáků navštěvuje všechny 3 kroužky? - Pravděpodobností 76764
 Prodavačka ojetých aut odhaduje, že pokaždé, když ukáže zákazníkovi auto, je pravděpodobnost 0,1, že zákazník auto koupí. Prodavačka by chtěla prodat alespoň jedno auto týdně. Pokud předvádění auta je Bernoulliho pokus s pravděpodobností 0,95 alespoň jedn
Prodavačka ojetých aut odhaduje, že pokaždé, když ukáže zákazníkovi auto, je pravděpodobnost 0,1, že zákazník auto koupí. Prodavačka by chtěla prodat alespoň jedno auto týdně. Pokud předvádění auta je Bernoulliho pokus s pravděpodobností 0,95 alespoň jedn - Euklid 9
 Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8
Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8 - Rovnají se
 Rovnají se následující výrazy? -9 10 = (-9) 10
Rovnají se následující výrazy? -9 10 = (-9) 10 - Z7-1-6 MO 2018
 Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt
Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt
