Čtyřboký jehlan
Pravidelný čtyřboký jehlan má délku podstavné hrany 6 cm a délka boční hrany je 9 centimetrů. Vypočítejte objem a obsah
Správná odpověď:
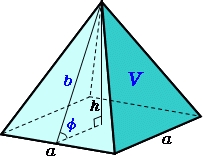
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- stereometrie
- jehlan
- povrch tělesa
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- čtyřúhelník
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Hrana
 Je dán pravidelný čtyřboký jehlan, délka podstavne hrany je 6 cm a výška jehlanu je 10 cm. Vypočítej délku boční hrany.
Je dán pravidelný čtyřboký jehlan, délka podstavne hrany je 6 cm a výška jehlanu je 10 cm. Vypočítej délku boční hrany. - Čtyřboký jehlan 4
 Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a = 3 cm a s délkou boční hrany h = 8 cm. Vypočítejte prosím jeho povrch a objem.
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a = 3 cm a s délkou boční hrany h = 8 cm. Vypočítejte prosím jeho povrch a objem. - Čtyřboký jehlan 9
 Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště.
Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště. - Pravidelný 81401
 Pravidelný čtyřboký jehlan má objem 2160 litrů a délku podstavné hrany 12dm. Vypočítej výšku jehlanu (náčrt, výpočet, odpověď).
Pravidelný čtyřboký jehlan má objem 2160 litrů a délku podstavné hrany 12dm. Vypočítej výšku jehlanu (náčrt, výpočet, odpověď). - Pravidelný 9
 Pravidelný čtyřboký jehlan má povrch 260 cm² a obsah jedné boční stěny 40 cm². Vypočítejte délku hrany podstavy a stěnovou výšku.
Pravidelný čtyřboký jehlan má povrch 260 cm² a obsah jedné boční stěny 40 cm². Vypočítejte délku hrany podstavy a stěnovou výšku. - Pravidelný 8109
 Pravidelný čtyřboký jehlan má úhlopříčku podstavy 5√2 cm a boční hrany mají délku 12√2 cm. Vypočítej výšku jehlanu a jeho povrch.
Pravidelný čtyřboký jehlan má úhlopříčku podstavy 5√2 cm a boční hrany mají délku 12√2 cm. Vypočítej výšku jehlanu a jeho povrch. - Pravidelný 11
 Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu
Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu - Je dán 21
 Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles.
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Vypočítej 40
 Vypočítej objem pravidelného čtyřbokého jehlanu, který má velikost podstavné hrany a = 8 cm a velikost boční hrany h = 9 cm.
Vypočítej objem pravidelného čtyřbokého jehlanu, který má velikost podstavné hrany a = 8 cm a velikost boční hrany h = 9 cm. - Šestiboký 6
 Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm. Vypočítej jeho objem.
Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm. Vypočítej jeho objem. - Pravidelný 8
 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Trojboký jehlan
 Vypočítejte objem a obsah pravidelného trojbokého jehlanu pokud výška jehlanu je 12 centimetrů, jehož hrana podstavy má 4 centimetry a výška boční stěny 12 cm.
Vypočítejte objem a obsah pravidelného trojbokého jehlanu pokud výška jehlanu je 12 centimetrů, jehož hrana podstavy má 4 centimetry a výška boční stěny 12 cm. - Pravidelný čtyřboký hranol
 Pravidelný čtyřboký hranol má hranu podstavy a=7,1 cm a boční hranu =18,2cm dlouhou. Vypočítejte jeho objem a povrch.
Pravidelný čtyřboký hranol má hranu podstavy a=7,1 cm a boční hranu =18,2cm dlouhou. Vypočítejte jeho objem a povrch. - Pravidelný 6332
 Pravidelný čtyřboký jehlan je vysoký 2m. Výška boční stěny je 2,8m. Jaké rozměry má podstava? Vypočítej povrch a objem jehlanu.
Pravidelný čtyřboký jehlan je vysoký 2m. Výška boční stěny je 2,8m. Jaké rozměry má podstava? Vypočítej povrch a objem jehlanu. - Vypočítejte 36
 Vypočítejte objem a povrch pravidelného šestibokého jehlanu o podstavné hraně a = 30 m a boční hraně b = 50 m.
Vypočítejte objem a povrch pravidelného šestibokého jehlanu o podstavné hraně a = 30 m a boční hraně b = 50 m. - Komolý
 Komolý pravidelný čtyřboký jehlan má objem 74 cm3, výšku v = 6 cm a obsah dolní podstavy o 15 cm² větší než obsah horní podstavy. Vypočítejte obsah horní podstavy.
Komolý pravidelný čtyřboký jehlan má objem 74 cm3, výšku v = 6 cm a obsah dolní podstavy o 15 cm² větší než obsah horní podstavy. Vypočítejte obsah horní podstavy. - Výška = hrana
 V pravidelném čtyřboký jehlanu se výška boční stěny rovná délce hrany podstavy. Obsah boční stěny je 32 cm². Jaký je povrch jehlanu?
V pravidelném čtyřboký jehlanu se výška boční stěny rovná délce hrany podstavy. Obsah boční stěny je 32 cm². Jaký je povrch jehlanu?
