Objem + úměra, poměr - příklady a úlohy
Počet nalezených příkladů: 141
- Pro objemy
 Pro objemy kolmého hranolu a jehlanu se stejnou podstavou a výškou platí: A) objemy jsou stejné B) objem jehlanu je třikrát menší než objem hranolu C) poměr objemů hranolu a jehlanu je 1:3 D)neplatí žádná z předchozích odpovědí
Pro objemy kolmého hranolu a jehlanu se stejnou podstavou a výškou platí: A) objemy jsou stejné B) objem jehlanu je třikrát menší než objem hranolu C) poměr objemů hranolu a jehlanu je 1:3 D)neplatí žádná z předchozích odpovědí - Povrch 33
 Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru.
Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru. - Objem 31
 Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru. - Objem 30
 Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru. - Je dán 21
 Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles.
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Máme roztok
 Máme 1 litr 80 % roztoku. Každou hodinu z roztoku vylijeme 1 dl a přilejeme 1 dl vody (což je 0% roztok) a promícháme. Kolikaprocentní roztok budeme mít po dvou mícháních?
Máme 1 litr 80 % roztoku. Každou hodinu z roztoku vylijeme 1 dl a přilejeme 1 dl vody (což je 0% roztok) a promícháme. Kolikaprocentní roztok budeme mít po dvou mícháních? - Krychli 4
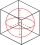 Krychli o objemu 4096cm³ je opsána a vepsána koule. Vypočítejte, kolikrát je větší objem opsané koule než koule vepsané.
Krychli o objemu 4096cm³ je opsána a vepsána koule. Vypočítejte, kolikrát je větší objem opsané koule než koule vepsané. - Máslo 4
 Průměrně je ze 100 litrů mléka 16 litrů smetany a ze 100 litrů smetany je 20 litrů másla. Kolik litrů mléka potřebujeme na 100 litrů másla?
Průměrně je ze 100 litrů mléka 16 litrů smetany a ze 100 litrů smetany je 20 litrů másla. Kolik litrů mléka potřebujeme na 100 litrů másla? - Pravidelného 83324
 Objem pravidelného čtyřbokého jehlanu je 72 cm³. Jeho výška se rovná délce podstavné hrany. Vypočítej délku podstavné a povrch jehlanu.
Objem pravidelného čtyřbokého jehlanu je 72 cm³. Jeho výška se rovná délce podstavné hrany. Vypočítej délku podstavné a povrch jehlanu. - Potřebuje 83225
 Malíř potřebuje smíchat žlutou a červenou barvu v poměru 3 : 7. Kolik litrů červené barvy musí přidat do 21 litrů žluté barvy?
Malíř potřebuje smíchat žlutou a červenou barvu v poměru 3 : 7. Kolik litrů červené barvy musí přidat do 21 litrů žluté barvy? - Akvárium 83135
 Velké akvárium má tvar kvádru, jehož rozměry jsou v poměru 5: 7: 4. Součet délek všech hran je 96 dm. Kolik litrů vody bude v akváriu, bude-li naplněno do čtyř pětin?
Velké akvárium má tvar kvádru, jehož rozměry jsou v poměru 5: 7: 4. Součet délek všech hran je 96 dm. Kolik litrů vody bude v akváriu, bude-li naplněno do čtyř pětin? - Vypočítej 83130
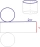 Vypočítej objem válce pokud víš, že poměr výšky válce a poloměru podstavy je 3:2 a výška má velikost 15 dm .
Vypočítej objem válce pokud víš, že poměr výšky válce a poloměru podstavy je 3:2 a výška má velikost 15 dm . - Nakreslením 83070
 Kužel o poloměru 10 cm je rozdělen na dvě části nakreslením roviny přes střed jeho osy, rovnoběžné s jeho základnou. Porovnejte objemy obou částí.
Kužel o poloměru 10 cm je rozdělen na dvě části nakreslením roviny přes střed jeho osy, rovnoběžné s jeho základnou. Porovnejte objemy obou částí. - Vyrobí 83037
 Z 20 hl mléka se vyrobí 8 kg. másla. Kolik kg másla se vyrobí ze 450 l mléka?
Z 20 hl mléka se vyrobí 8 kg. másla. Kolik kg másla se vyrobí ze 450 l mléka? - Zůstala 82495
 V čajníku byly 2 litry čaje. Táta si nalil čtvrt litru, máma půl litru čaje. Jaká část zůstala v čajníku?
V čajníku byly 2 litry čaje. Táta si nalil čtvrt litru, máma půl litru čaje. Jaká část zůstala v čajníku? - Pomerančové 82303
 Juraj měl v láhvi 1 litr čisté pomerančové šťávy. Odlil z ní 2 decilitry a nahradil ji vodou. Jaký je nyní poměr pomerančové šťávy a vody v láhvi?
Juraj měl v láhvi 1 litr čisté pomerančové šťávy. Odlil z ní 2 decilitry a nahradil ji vodou. Jaký je nyní poměr pomerančové šťávy a vody v láhvi? - 2-taktní 81945
 2-taktní motory vyžadují pro správný chod směs oleje a plynu. Na každý galon plynu vyžaduje určitý 2-taktní motor 1 1/4 fl oz oleje. Kolik oleje se musí přidat na přípravu 3 1/2 galonu plynu, aby se získala správná směs?
2-taktní motory vyžadují pro správný chod směs oleje a plynu. Na každý galon plynu vyžaduje určitý 2-taktní motor 1 1/4 fl oz oleje. Kolik oleje se musí přidat na přípravu 3 1/2 galonu plynu, aby se získala správná směs? - Používala 81805
 Mýdlo má tvar kvádru o rozměrech 6cm, 4cm a 2cm. Katka jej používala týden a všechny rozměry mýdla se zmenšily právě na polovinu. Jak dlouho jí ještě mýdlo vydrží?
Mýdlo má tvar kvádru o rozměrech 6cm, 4cm a 2cm. Katka jej používala týden a všechny rozměry mýdla se zmenšily právě na polovinu. Jak dlouho jí ještě mýdlo vydrží? - Přesýpací hodiny
 Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
