Objem + procenta - příklady a úlohy
Počet nalezených příkladů: 204
- Chemické výpočty
 50% roztok soli je třeba naředit destilovanou vodou tak, aby vzniklo 20 litrů 35% roztoku. Kolik litrů původního roztoku a kolik litrů vody potřebujeme?
50% roztok soli je třeba naředit destilovanou vodou tak, aby vzniklo 20 litrů 35% roztoku. Kolik litrů původního roztoku a kolik litrů vody potřebujeme? - Kuchyňský
 Kuchyňský ocet je 8% roztok kyseliny octové ve vodě. Kolik litrů kyseliny octové je třeba na výrobu 275 l octa?
Kuchyňský ocet je 8% roztok kyseliny octové ve vodě. Kolik litrů kyseliny octové je třeba na výrobu 275 l octa? - Jaké množství
 Jaké množství betonu je třeba objednat pro vybetonování rodinného domu obdélníkového půdorysu o rozměrech 15 m × 12,6 m při použití ztraceného bednění. Hloubka základů tvořený ztracenými bedněním je stanovena na 80cm. Použitý beton tvoří 80% objemu tvárni
Jaké množství betonu je třeba objednat pro vybetonování rodinného domu obdélníkového půdorysu o rozměrech 15 m × 12,6 m při použití ztraceného bednění. Hloubka základů tvořený ztracenými bedněním je stanovena na 80cm. Použitý beton tvoří 80% objemu tvárni - Vápno
 Jáma na vápno má tvar čtyřbokého hranolů s rozměry 2m, 1,8m a 1,5m Vypočitajte objem hromady z vykopané zeminy, který v důsledku načechraní je o 20% větší než objem jámy.
Jáma na vápno má tvar čtyřbokého hranolů s rozměry 2m, 1,8m a 1,5m Vypočitajte objem hromady z vykopané zeminy, který v důsledku načechraní je o 20% větší než objem jámy. - Kolik 139
 Kolik cihel je potřeba na stavbu zdi, která má délku 12 m, výšku 1,6 m a šířku 47 cm, je-li rozměr cihly 30 x 15 x 7,5 cm a 5 % objemu zdi tvoří malta?
Kolik cihel je potřeba na stavbu zdi, která má délku 12 m, výšku 1,6 m a šířku 47 cm, je-li rozměr cihly 30 x 15 x 7,5 cm a 5 % objemu zdi tvoří malta? - Koule 25
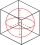 Koule o průměru 10 cm je v krabičce tvaru krychle o hraně 10cm. Kolik procent krabičky koule vyplňuje?
Koule o průměru 10 cm je v krabičce tvaru krychle o hraně 10cm. Kolik procent krabičky koule vyplňuje? - Teplá 3
 Teplá kapalina v nádobě po vychladnutí zmenšila svůj objem o 2/27 O kolik procent byl objem teplé kapaliny větší než objem vychladlé kapaliny?
Teplá kapalina v nádobě po vychladnutí zmenšila svůj objem o 2/27 O kolik procent byl objem teplé kapaliny větší než objem vychladlé kapaliny? - Do rovnostranného 2
 Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule?
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Máme roztok
 Máme 1 litr 80 % roztoku. Každou hodinu z roztoku vylijeme 1 dl a přilejeme 1 dl vody (což je 0% roztok) a promícháme. Kolikaprocentní roztok budeme mít po dvou mícháních?
Máme 1 litr 80 % roztoku. Každou hodinu z roztoku vylijeme 1 dl a přilejeme 1 dl vody (což je 0% roztok) a promícháme. Kolikaprocentní roztok budeme mít po dvou mícháních? - Skleník 2
 Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr
Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr - Modelovací 83173
 Modelovací hmota ztrácí usušením 36% z původního objemu. Jakou délku měla původně hrana kostky, když po usušení má kostka objem 5,12 dm³?
Modelovací hmota ztrácí usušením 36% z původního objemu. Jakou délku měla původně hrana kostky, když po usušení má kostka objem 5,12 dm³? - Zmenšíme 82810
 Kvádr má rozměry 10cm, 20cm a 50cm. První hranu kvádru zmenšíme o 20% a druhou o 20% zvětšíme. Jak se změní objem kvádru? O kolik procent?
Kvádr má rozměry 10cm, 20cm a 50cm. První hranu kvádru zmenšíme o 20% a druhou o 20% zvětšíme. Jak se změní objem kvádru? O kolik procent? - Sirupu 82335
 Máme 4,5 litru sirupu, a 80% tvoří šťáva. Kolik litrů bylo šťávy?
Máme 4,5 litru sirupu, a 80% tvoří šťáva. Kolik litrů bylo šťávy? - Energetickou 81620
 Energie se měří pomocí jednotky Joule (J). Teplota se měří pomocí jednotky stupně Celsia °C). Ke zvýšení teploty 1 litru vody o 1°C je zapotřebí 4200 J tepelné energie. (a) Kelly chce zvýšit teplotu 2 litrů vody z 25°C na 100°C. (1) Najděte množství potře
Energie se měří pomocí jednotky Joule (J). Teplota se měří pomocí jednotky stupně Celsia °C). Ke zvýšení teploty 1 litru vody o 1°C je zapotřebí 4200 J tepelné energie. (a) Kelly chce zvýšit teplotu 2 litrů vody z 25°C na 100°C. (1) Najděte množství potře - Procentech 81558
 Do 100 litrů vody nalijeme 9 dl barviva. Jaký bude podíl barviva ve výsledné směsi? Vyjádři v procentech
Do 100 litrů vody nalijeme 9 dl barviva. Jaký bude podíl barviva ve výsledné směsi? Vyjádři v procentech - Chceme-li 81397
 Dětský bazén má tvar válce o průměru podstavy 4 m a hloubce 50 cm (náčrt, výpočet, odpověď). a) Vypočítej objem vody v litrech, který může být v bazénu, je-li naplněn po okraj. b) Pokud bazén naplníme jen na 75%, kolik litrů vody bude v bazénu? c) Chceme-
Dětský bazén má tvar válce o průměru podstavy 4 m a hloubce 50 cm (náčrt, výpočet, odpověď). a) Vypočítej objem vody v litrech, který může být v bazénu, je-li naplněn po okraj. b) Pokud bazén naplníme jen na 75%, kolik litrů vody bude v bazénu? c) Chceme- - Litrového 81334
 Číšník ráno má 200 sklenic o objemu 0,3 litru a 100 sklenic velkých o objemu každý 0,5 litrů. Začne čepovat do těch sklenic ze 100 litrového sudu. Večer mu zůstane polovina z těch malých piv a z velkých pětina. Kolik % mu zůstane v sudu?
Číšník ráno má 200 sklenic o objemu 0,3 litru a 100 sklenic velkých o objemu každý 0,5 litrů. Začne čepovat do těch sklenic ze 100 litrového sudu. Večer mu zůstane polovina z těch malých piv a z velkých pětina. Kolik % mu zůstane v sudu? - Vody/přípravku 81313
 Příklad č. | 1: Na přípravu 2%-ního roztoku potřebujeme 20 l vody. Kolik ml přípravku spotřebujeme? Příklad č. | 2: Kolik litrů vody/přípravku potřebujeme na přípravu 20 litrů 2% roztoku? Příklad č. | 3: Kolik litrů vody potřebujeme na přípravu 2% roztoku
Příklad č. | 1: Na přípravu 2%-ního roztoku potřebujeme 20 l vody. Kolik ml přípravku spotřebujeme? Příklad č. | 2: Kolik litrů vody/přípravku potřebujeme na přípravu 20 litrů 2% roztoku? Příklad č. | 3: Kolik litrů vody potřebujeme na přípravu 2% roztoku - O kolik 12
 O kolik procent se zmenší objem krychle, zmenší-li se délka její hrany o čtvrtinu?
O kolik procent se zmenší objem krychle, zmenší-li se délka její hrany o čtvrtinu? - Mléko a máslo
 Kravské mléko obsahuje průmerně 3,6% tuku. Kolik litrů mléka je potřeba na výrobu 250g másla? Máslo obsahuje 82% tuku.
Kravské mléko obsahuje průmerně 3,6% tuku. Kolik litrů mléka je potřeba na výrobu 250g másla? Máslo obsahuje 82% tuku.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
