Obsah + povrch tělesa - příklady a úlohy
Počet nalezených příkladů: 487
- Věžička 2
 Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn
Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn - Paní učitelka
 Paní učitelka se rozhodla, že ušije na osm sedacích kostek ve školní knihovně potahy. Všechny kostky mají tvar krychle s hranou dlouhou 40 cm. Kolik celých m² látky bude paní učitelka celkem potřebovat, pokud kostky nebudou povlečeny zespodu a je třeba př
Paní učitelka se rozhodla, že ušije na osm sedacích kostek ve školní knihovně potahy. Všechny kostky mají tvar krychle s hranou dlouhou 40 cm. Kolik celých m² látky bude paní učitelka celkem potřebovat, pokud kostky nebudou povlečeny zespodu a je třeba př - Skleník 2
 Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr
Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr - 1 kg cukru
 1 kg kostkového cukru je tvořeno 840 krychlička o hraně 1,1 cm. Určete hustotu cukru a rozměr krabice jsou-li krychličky narovnány v sedmi řadách po devíti kostičkách. Kolik čtverečních metrů kartónu je třeba na výrobu 3000 těchto krabic?
1 kg kostkového cukru je tvořeno 840 krychlička o hraně 1,1 cm. Určete hustotu cukru a rozměr krabice jsou-li krychličky narovnány v sedmi řadách po devíti kostičkách. Kolik čtverečních metrů kartónu je třeba na výrobu 3000 těchto krabic? - Sklěněné 2
 Sklěněné vánoční ozdoby mají tvar koule s průměrem 8cm. V malé rodinné firmě jich ročně vyrobí 50000 kusů. celý povrch těchto koulí je pokryt třpytkami. Na pokrytí plochy 1m² je potřeba 400 g třpytek. Kolik kilogramu třpytek je potřeba k pokrytí všech vyr
Sklěněné vánoční ozdoby mají tvar koule s průměrem 8cm. V malé rodinné firmě jich ročně vyrobí 50000 kusů. celý povrch těchto koulí je pokryt třpytkami. Na pokrytí plochy 1m² je potřeba 400 g třpytek. Kolik kilogramu třpytek je potřeba k pokrytí všech vyr - Obvod 34
 Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm².
Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm². - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Stínítko
 Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem
Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem - Papírová
 Papírová krabice má tvar krychle. Na její výrobu bylo spotřebováno 2400 cm².Ohyby pro přilepení stěn se nezapočítávají. Jaký je objem krabice?
Papírová krabice má tvar krychle. Na její výrobu bylo spotřebováno 2400 cm².Ohyby pro přilepení stěn se nezapočítávají. Jaký je objem krabice? - Objem 30
 Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru. - Kulová úseč 4
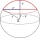 Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm.
Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm. - Povrch 33
 Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru.
Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru. - Objem 31
 Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru. - Výroky
 Výroky se prodávají v kartonových krabicích – např. krabice na mikrovlnnou troubu má rozměry 52 cm, 32 cm a 40 cm a na záhyby se přidává 0,4 m² kartonu. Kolik m² kartonu je třeba na 1 000 krabic?
Výroky se prodávají v kartonových krabicích – např. krabice na mikrovlnnou troubu má rozměry 52 cm, 32 cm a 40 cm a na záhyby se přidává 0,4 m² kartonu. Kolik m² kartonu je třeba na 1 000 krabic? - Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - Truhlář 5
 Truhlář opracovával rotační válec s poloměrem podstavy 2,5dm a výškou 2dm. Rovnoměrným broušením zmenšil poloměr o 1cm, výška válce byla zachována. Vypocitej, o kolik procent se zmenšil obsah válce.
Truhlář opracovával rotační válec s poloměrem podstavy 2,5dm a výškou 2dm. Rovnoměrným broušením zmenšil poloměr o 1cm, výška válce byla zachována. Vypocitej, o kolik procent se zmenšil obsah válce. - Válec 27
 Válec má stejný průměr jako výšku. Vypočítejte tyto údaje. je-li povrch 200 cm čtverečních. Výsledky uveďte s přesností na milimetry
Válec má stejný průměr jako výšku. Vypočítejte tyto údaje. je-li povrch 200 cm čtverečních. Výsledky uveďte s přesností na milimetry - Na sklenice
 Na sklenice chceme přilepit etikety. Etikety se lepí přesně kolem sklenice. Průměr sklenice je 6cm. Výška etikety je 10cm. a) Kolik etiket vyrobíme z papíru o rozměru 30 x 40cm? b) Z kolika papíru tohoto rozměru vyrobíme 100 etiket?
Na sklenice chceme přilepit etikety. Etikety se lepí přesně kolem sklenice. Průměr sklenice je 6cm. Výška etikety je 10cm. a) Kolik etiket vyrobíme z papíru o rozměru 30 x 40cm? b) Z kolika papíru tohoto rozměru vyrobíme 100 etiket?
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
